|
错解剖析得真知（一） 第一章 集合与常用逻辑用语 §1.1 集合的概念与运算 一、知识导学 1.集合：一般地，一定范围内某些确定的、不同的对象的全体构成一个集合. 2.元素：集合中的每一个对象称为该集合的元素，简称元. 3.子集：如果集合A的任意一个元素都是集合B的元素（若  则 ），则称集合A为集合B的子集，记为A  B或B A；如果AB，并且A B，这时集合A称为集合B的真子集，记为A B或B A.4.集合的相等：如果集合A、B同时满足A B、BA，则A=B.5.补集：设A S，由S中不属于A的所有元素组成的集合称为S的子集A的补集，记为  .6.全集：如果集合S包含所要研究的各个集合，这时S可以看做一个全集，全集通常 记作U. 7.交集：一般地，由所有属于集合A且属于B的元素构成的集合，称为A与B的交集， 记作A  B.8.并集：一般地，由所有属于集合A或者属于B的元素构成的集合，称为A与B的并 集，记作A  B.9.空集：不含任何元素的集合称为空集，记作  .10.有限集：含有有限个元素的集合称为有限集. 11.无限集：含有无限个元素的集合称为无限集. 12.集合的常用表示方法：列举法、描述法、图示法（Venn图）. 13.常用数集的记法：自然数集记作N，正整数集记作N+或N  ，整数集记作Z，有理数集记作Q，实数集记作R. 二、疑难知识导析 1.符号 ，，，，=，表示集合与集合之间的关系，其中“”包括“”和“=”两种情况，同样“”包括“ ”和“=”两种情况.符号 ， 表示元素与集合之间的关系.要注意两类不同符号的区别.2.在判断给定对象能否构成集合时，特别要注意它的“确定性”，在表示一个集合时，要特别注意它的“互异性”、“无序性”. 3.在集合运算中必须注意组成集合的元素应具备的性质. 4.对由条件给出的集合要明白它所表示的意义，即元素指什么，是什么范围．用集合表示不等式（组）的解集时，要注意分辨是交集还是并集，结合数轴或文氏图的直观性帮助思维判断．空集是任何集合的子集，但因为不好用文氏图形表示，容易被忽视，如在关系式  中，B=易漏掉的情况. 5.若集合中的元素是用坐标形式表示的，要注意满足条件的点构成的图形是什么，用数形结合法解之. 6.若集合中含有参数，须对参数进行分类讨论，讨论时既不重复又不遗漏. 7.在集合运算过程中要借助数轴、直角坐标平面、Venn图等将有关集合直观地表示出来. 8.要注意集合与方程、函数、不等式、三角、几何等知识的密切联系与综合使用. 9.含有n个元素的集合的所有子集个数为：  ，所有真子集个数为：-1 三、经典例题导讲 [例1] 已知集合M={y|y =x2＋1,x∈R},N={y|y =x＋1,x∈R}，则M∩N=（ ） A．（0，1），（1，2） B．{（0，1），（1，2）} C．{y|y=1,或y=2} D．{y|y≥1} 错解：求M∩N及解方程组  得 或  ∴选B错因：在集合概念的理解上，仅注意了构成集合元素的共同属性，而忽视了集合的元素是什么．事实上M、N的元素是数而不是实数对(x,y)，因此M、N是数集而不是点集, M、N分别表示函数y=x2＋1(x∈R)，y=x＋1(x∈R)的值域，求M∩N即求两函数值域的交集． 正解：M={y|y=x2＋1,x∈R}={y|y≥1}， N={y|y=x＋1,x∈R}={y|y∈R}． ∴M∩N={y|y≥1}∩{y|(y∈R)}={y|y≥1}, ∴应选D． 注：集合是由元素构成的，认识集合要从认识元素开始，要注意区分{x|y=x2＋1}、{y|y=x2＋1,x∈R}、{(x,y)|y=x2＋1,x∈R}，这三个集合是不同的． [例2] 已知A={x|x2－3x＋2=0},B={x|ax－2=0}且A∪B=A，求实数a组成的集合C． 错解：由x2－3x＋2=0得x=1或2． 当x=1时，a=2， 当x=2时，a=1． 错因：上述解答只注意了B为非空集合，实际上，B=  时，仍满足A∪B=A.当a=0时，B= ，符合题设，应补上，故正确答案为C={0，1，2}．正解：∵A∪B=A ∴B  A 又A={x|x2－3x＋2=0}={1，2}∴B= 或 ∴C={0，1，2}[例3]已知m A,nB, 且集合A= ，B= ，又C= ，则有： （ ）A．m+n A B. m+nB C.m+nC D. m+n不属于A，B，C中任意一个错解：∵m A，∴m=2a,a ,同理n=2a+1,aZ, ∴m+n=4a+1,故选C错因是上述解法缩小了m+n的取值范围. 正解：∵m A, ∴设m=2a1,a1Z, 又∵n ,∴n=2a2+1,a2 Z ,∴m+n=2(a1+a2)+1,而a1+a2 Z , ∴m+nB, 故选B.[例4］ 已知集合A={x|x2－3x－10≤0}，集合B={x|p＋1≤x≤2p－1}．若B A，求实数p的取值范围．错解：由x2－3x－10≤0得－2≤x≤5． 欲使B A，只须 ∴ p的取值范围是－3≤p≤3. 错因：上述解答忽略了"空集是任何集合的子集"这一结论，即B= 时，符合题设． 正解：①当B≠ 时，即p＋1≤2p－1 p≥2.由B A得：－2≤p＋1且2p－1≤5.由－3≤p≤3. ∴ 2≤p≤3 ②当B= 时，即p＋1>2p－1p＜2.由①、②得：p≤3. 点评：从以上解答应看到：解决有关A∩B= 、A∪B=，AB等集合问题易忽视空集的情况而出现漏解，这需要在解题过程中要全方位、多角度审视问题．[例5] 已知集合A={a,a＋b,a＋2b}，B={a,ac,ac2}．若A=B，求c的值． 分析：要解决c的求值问题，关键是要有方程的数学思想，此题应根据相等的两个集合元素完全相同及集合中元素的确定性、互异性，无序性建立关系式． 解：分两种情况进行讨论． （1）若a＋b=ac且a＋2b=ac2，消去b得：a＋ac2－2ac=0， a=0时，集合B中的三元素均为零，和元素的互异性相矛盾，故a≠0． ∴c2－2c＋1=0，即c=1，但c=1时，B中的三元素又相同，此时无解． （2）若a＋b=ac2且a＋2b=ac，消去b得：2ac2－ac－a=0， ∵a≠0，∴2c2－c－1=0， 即(c－1)(2c＋1)=0，又c≠1，故c=－  ．点评：解决集合相等的问题易产生与互异性相矛盾的增解，这需要解题后进行检验. [例6] 设A是实数集，满足若a∈A，则  A， 且1?A.⑴若2∈A，则A中至少还有几个元素？求出这几个元素. ⑵A能否为单元素集合？请说明理由. ⑶若a∈A，证明：1－  ∈A.⑷求证：集合A中至少含有三个不同的元素. 解：⑴2∈A ? －1∈A ? ∈A ? 2∈A∴ A中至少还有两个元素：－1和 ⑵如果A为单元素集合，则a＝ 即  ＝0该方程无实数解，故在实数范围内，A不可能是单元素集 ⑶a∈A ? 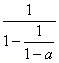∈A ?  ∈A? A，即1－∈A⑷由⑶知a∈A时， ∈A， 1－∈A .现在证明a,1－, 三数互不相等.①若a=,即a2-a+1=0 ，方程无解，∴a≠②若a=1－ ，即a2-a+1=0，方程无解∴a≠1－ ③若1－ =，即a2-a+1=0，方程无解∴1－≠.综上所述，集合A中至少有三个不同的元素. 点评：⑷的证明中要说明三个数互不相等，否则证明欠严谨. [例7] 设集合A={  |= , ∈N+}，集合B={ |= , ∈N+}，试证：AB．证明：任设 ∈A， 则 ==(＋2)2－4(＋2)＋5 (∈N+),∵ n∈N*，∴ n＋2∈N* ∴ a∈B故  ①显然，1  ，而由B={ |=,∈N+}={|= ，∈N+}知1∈B，于是A≠B ②由①、② 得A B．点评：（1）判定集合间的关系，其基本方法是归结为判定元素与集合之间关系． （2）判定两集合相等，主要是根据集合相等的定义． 四、典型习题导练 1．集合A={x|x2－3x－10≤0，x∈Z}，B={x|2x2－x－6＞0， x∈ Z}，则A∩B的非空真子集的个数为（ ） A．16 B．14 C．15 D．32 2．数集{1，2，x2－3}中的x不能取的数值的集合是（ ） A．{2，-2 } B．{－2，－  } C．{±2，± } D．{，－}3. 若P={y|y=x2,x∈R}，Q={y|y=x2＋1,x∈R}，则P∩Q等于（ ） A．P B．Q C． D．不知道4. 若P={y|y=x2,x∈R}，Q={(x，y)|y=x2,x∈R}，则必有（ ） A．P∩Q= B．P Q C．P=Q D．P Q5．若集合M＝｛  ｝，N＝{ | ≤}，则M N＝ （ ）A．  B． C．  D． 6.已知集合A={x|x2＋(m＋2)x＋1=0,x∈R}，若A∩R＋= ，则实数m的取值范围是_________．7.（06高考全国II卷）设  ，函数 若 的解集为A， ，求实数的取值范围.8.已知集合A=  和B= 满足 A∩B= ，A∩B= ，I=R，求实数a,b的值.§1.2．常用逻辑用语 一、知识导学 1．逻辑联结词：“且”、“或”、 “非”分别用符号“  ”“ ”“ ”表示.2．命题：能够判断真假的陈述句． 3．简单命题：不含逻辑联结词的命题 4．复合命题：由简单命题和逻辑联结词构成的命题，复合命题的基本形式：p或q；p且q；非p 5．四种命题的构成：原命题：若p则q； 逆命题：若q则p；否命题：若  p 则q ；逆否命题：若q 则p.6．原命题与逆否命题同真同假，是等价命题，即“若p则q”  “若q 则p ” .7．反证法：欲证“若p则q”，从“非q”出发，导出矛盾，从而知“若p则非q”为假，即“若p则q”为真 . 8．充分条件与必要条件： ①p  q ：p是q的充分条件；q是p的必要条件； ②p q ：p是q的充要条件 . 9．常用的全称量词：“对所有的”、“ 对任意一个”“ 对一切”“ 对每一个”“任给”等；并用符号“  ” 表示.含有全称量词的命题叫做全称命题.10．常用的存在量词：“存在一个”、“至少有一个”、“有些”、“有一个”、 “有的”、“对某个”； 并用符号“  ”表示.含有存在量词的命题叫做特称命题.二、疑难知识导析 1．基本题型及其方法 （1）由给定的复合命题指出它的形式及其构成； （2）给定两个简单命题能写出它们构成的复合命题，并能利用真值表判断复合命题的真假； （3）给定命题，能写出它的逆命题、否命题、逆否命题，并能运用四种命题的相互关系，特别是互为逆否命题的等价性判断命题的真假.注意：否命题与命题的否定是不同的. （4）判断两个命题之间的充分、必要、充要关系； 方法：利用定义 （5）证明  的充要条件是 ；方法：分别证明充分性和必要性 （6）反证法证题的方法及步骤：反设、归谬、结论.反证法是通过证明命题的结论的反面不成立而肯定命题的一种数学证明方法，是间接证法之一. 注：常见关键词的否定：
2．全称命题与特称命题的关系： 全称命题p:  ,它的否定 : ；特称命题p: ,它的否定: ；即全称命题的否定是特称命题，特称命题的否定是全称命题.否定一个全称命题可以通过“举反例”来说明.三、经典例题导讲 [例1] 把命题“全等三角形一定相似”写成“若p则q”的形式，并写出它的逆命题、否命题与逆否命题. 错解：原命题可改写成：若两个三角形全等，则它们一定相似. 逆命题：若两个三角形相似，则它们全等. 否命题：若两个三角形不一定全等，则它们不一定相似. 逆否命题：若两个三角形不一定相似，则它们不一定全等. 错因：对“一定”的否定把握不准，“一定”的否定 “一定不”，在逻辑知识中求否定相当于求补集，而“不一定”含有“一定”的意思.对这些内容的学习要多与日常生活中的例子作比较，注意结合集合知识.因而否命题与逆否命题错了. 正解：否命题：若两个三角形不全等，则它们不相似. 逆否命题：若两个三角形不相似，则它们不全等. [例2] 将下列命题改写成“若p则q”的形式，并写出否命题.a>o时，函数y=ax+b的值随x值的增加而增加. 错解：原命题改为：若a>o时，x的值增加，则函数y=ax+b的值也随着增加. 错因：如果从字面上分析最简单的方法是将a>o看作条件，将“随着”看作结论，而x的值增加，y的值也增加看作研究的对象，那么原命题改为若a>o时，则函数y=ax+b的值随着x的值增加而增加，其否命题为若a  o时，则函数y=ax+b的值不随x值的增加而增加.此题错解在注意力集中在“增加”两个字上，将x值的增加当做条件，又不把a>o看作前提，就变成两个条件的命题，但写否命题时又没按两个条件的规则写，所以就错了.正解：原命题改为： a>o时，若x的值增加，则函数y=ax+b的值也随着增加. 否命题为： a>o时，若x的值不增加，则函数y=ax+b的值也不增加. 原命题也可改为：当x的值增加时，若a>o，，则函数y=ax+b的值也随着增加. 否命题为： 当x增加时，若a o，则函数y=ax+b的值不增加.[例3] 已知h>0，设命题甲为：两个实数a、b满足  ，命题乙为：两个实数a、b满足 且 ，那么A．甲是乙的充分但不必要条件 B．甲是乙的必要但不充分条件 C．甲是乙的充要条件 D．甲是乙的既不充分也不必要条件 错解：    , 故本题应选C. 错因：（1）对充分、必要、充要条件的概念分不清，无从判断，凭猜测产生错误； （2）不能运用绝对值不等式性质作正确推理而产生错误. 正解：因为  所以 两式相减得  故 即由命题甲成立推出命题乙成立，所以甲是乙的必要条件. 由于 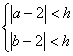 同理也可得 因此，命题甲成立不能确定命题乙一定成立，所以甲不是乙的充分条件，故应选B. [例4] 已知命题甲：a+b 4, 命题乙:a 且b ，则命题甲是命题乙的 .错解：由逆否命题与原命题同真同假知，若a=1且b=3则a+b=4成立，所以命题甲是命题乙的充分不必要条件. 错因 ：对命题的否定不正确.a 且b的否定是a=1或b=3.正解：当a+b 4时,可选取a=1,b=5，故此时a且b不成立( a=1).同样，a ,且b时，可选取a=2,b=2,a+b=4，故此时a+b=4.因此，甲是乙的既不充分也不必要条件. 注：a 且b为真时，必须a,b同时成立.[例5] 已知p是r的充分不必要条件，s是r的必要条件，q是s的必要条件，那么p是q成立的 ( ) A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件 分析：本题考查简易逻辑知识. 因为p  rsq但r成立不能推出p成立，所以 ,但q成立不能推出p成立，所以选A解：选A [例6] 已知关于x的一元二次方程 (m∈Z) ① mx2－4x＋4＝0 ② x2－4mx＋4m2－4m－5＝0 求方程①和②都有整数解的充要条件. 解：方程①有实根的充要条件是  解得m1.方程②有实根的充要条件是  ，解得  故m=－1或m=0或m=1. 当m=－1时，①方程无整数解.当m=0时，②无整数解； 当m=1时，①②都有整数.从而①②都有整数解m=1.反之，m=1①②都有整数解. ∴①②都有整数解的充要条件是m=1. [例7] 用反证法证明：若 、、  ，且 ， ， ，则、 、 中至少有一个不小于0 证明： 假设 、、均小于0，即： ----① ；  ----② ；  ----③；①+②+③得  ，这与  矛盾，则假设不成立， ∴ 、、中至少有一个不小于0.[例8] 已知命题p:方程x2＋mx＋1=0有两个不等的负根；命题q:方程4x2＋4(m－2)x＋1＝0无实根．若“p或q”为真，“p且q”为假，求m的取值范围． 分析：“p或q”为真，则命题p、q至少有一个为真，“p且q”为假，则命题p、q至少有一为假，因此，两命题p、q应一真一假，即命题p为真，命题q为假或命题p为假，命题q为真. 解： 若方程x2＋mx＋1=0有两不等的负根，则  解得m＞2，即命题p：m＞2 若方程4x2＋4(m－2)x＋1＝0无实根， 则Δ＝16(m－2)2－16＝16(m2－4m＋3)＜0 解得：1＜m＜3.即q：1＜m＜3. 因“p或q”为真，所以p、q至少有一为真， 又“p且q”为假，所以命题p、q至少有一为假， 因此，命题p、q应一真一假，即命题p为真，命题q为假或命题p为假，命题q为真. ∴  解得：m≥3或1＜m≤2. 四、典型习题导练 1．方程  至少有一个负根，则（ ）A.  或 B. C. D. 2．“  ”是“ 或 ”的（ ）A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 3．三个数  不全为0的充要条件是 （ ）A. 都不是0. B.中至多一个是0.C. 中只有一个是0. D.中至少一个不是0.4．由命题p:6是12的约数，q:6是24的约数，构成的“p或q”形式的命题是：_ ___，“p且q”形式的命题是__ _，“非p”形式的命题是__ _. 5．若  ，试从A.  B. C. D. E. F. 中，选出适合下列条件者，用代号填空：（1）使  都为0的充分条件是 ；（2）使 都不为0的充分条件是 ；（3）使 中至少有一个为0的充要条件是 ；（4）使 中至少有一个不为0的充要条件是 ．6．分别指出由下列各组命题构成的逻辑关联词“或”、“且”、“非”的真假． （1）p: 梯形有一组对边平行；q：梯形有一组对边相等． （2）p: 1是方程  的解；q：3是方程的解．（3）p: 不等式  解集为R；q: 不等式 解集为 ．7．命题：已知a、b为实数，若x2＋ax＋b≤0 有非空解集，则a2－ 4b≥0.写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假． 8．用反证法证明：若a、b、c、d均为小于1的正数，且x=4a(1－b)，y=4b(1－c)，z=4c(1－d)，t=4d(1－a)，则x、y、z、t四个数中，至少有一个不大于1． (责任编辑：admin) |
（
）
）