|
高中数学竞赛讲义(十一)答案 基础训练题 1.圆。设AO交圆于另一点 2.圆或椭圆。设给定直线为y=±kx(k>0),P(x,y)为轨迹上任一点,则 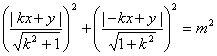 。化简为2k2x2+2y2=m2(1+k2). 。化简为2k2x2+2y2=m2(1+k2).当k≠1时,表示椭圆;当k=1时,表示圆。 3.12.由题设a=10,b=6,c=8,从而P到左焦点距离为10e=10× 4.-2<k<2或k<5.由(|k|-2)(5-k)<0解得k>5或-2<k<2. 5. 6.3x+4y-5=0.设M(x1,y1),N(x2,y2),则 7.-4.设B(x1,y1),C(x2,y2),则  8. 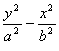 =1。由平移公式 =1。由平移公式9.2.曲线y2=ax关于点(1,1)的对称曲线为(2-y)2=a(2-x), 由 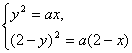 得y2-2y+2-a=0,故y1+y2=2,从而 得y2-2y+2-a=0,故y1+y2=2,从而10.(2, ,|PF2|=ex1-a,|PF1|+|PF2|=2ex1, 所以 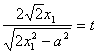 ,即 ,即11.解:由对称性,不妨设点P在第一象限,由题设|F1F2|2=4 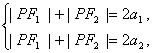 解得|PF1|=a1+a2,|PF2|=a1-a2. 解得|PF1|=a1+a2,|PF2|=a1-a2.在ΔF1PF2中,由余弦定理 从而 又sin∠F1PF2= 所以 12.解:以直线AB为x轴,AT的中垂线为y轴建立直角坐标系,则由定义知M,N两点既在抛物线y2=4ax上,又在圆[x-(a+r)]2+y2=r2上,两方程联立得x2+(2a-2r)x+2ra+a2=0,设点M,N坐标分别为(x1,y1),(x2,y2),则x1+x2=2r-2a.又|AM|=|MP|=x1+a,|AN|=|NP|=x2+a. |AB|=2r,所以 |AM|+|AN|=x1+x2+2a=2r=|AB|. 得证。 13.解:若直线l垂直于x轴,因其过点A(2,1),根据对称性,P1P2的中点为(2,0)。 若l不垂直于x轴,设l的方程为y-1=k(x-2),即 y=kx+1-2k. ① 将①代入双曲线方程消元y得 (2-k2)x2+2k(2k-1)x-(4k2-4k+3)=0. ② 这里 设x1,x2是方程②的两根,由韦达定理 由①,③得 y1+y2=kx1+(1-2k)+kx2+(1-2k) =k(x1+x2)+2(1-2k)= 设P1P2的中点P坐标(x,y),由中点公式及③,④得 消去k得 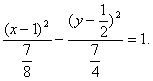 点(2,0)满足此方程,故这就是点P的轨迹方程。 高考水平测试题 1. 2. 900。见图1,由定义得|FA|=|AA1|,|FB|=|BB1|,有∠1=∠BFB1,∠2=∠AFA1,又∠1=∠3,∠2=∠4,所以∠3+∠4=∠BFB1+∠AFA1=900。 3.相切,若P(x,y)在左支上,设F1为左焦点,F2为右焦点,M为PF1中点,则|MO|= 4. 5.充要。将y=2x+1代入椭圆方程得(b2+4a2)x2+4a2x+a2 (1-b2)=0. ① 若Δ=(4a2) 2-4(b2+4a2)a2 (1-b2)=0,则直线与椭圆仅有一个公共点,即b2+4a2=1;反之,4a2+b2=1,直线与椭圆有一个公共点。 6.y=2(x-1)。消去参数得(y-2m) 2=4(x-m),焦点为 7.1≤m<5。直线过定点(0,1),所以0 8.3.双曲线实轴长为6,通径为4,故线段端点在异支上一条,在同支上有二条,一共有三条。 9. 因F(1,0),AF x1x2-(x1+x2)+1+k2x1x2=0. ③ 把①,②代入③得 10.3.首先这样的三角形一定存在,不妨设A,B分别位于y轴左、右两侧,设CA斜率为k(k>0),CA的直线方程为y=kx+1,代入椭圆方程为(a2k2+1)x2+2a2kx=0,得x=0或 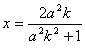 ,于是 ,于是由题设,同理可得|CB|= (k-1)[k2-(a2-1)k+1]=0, 解得 k=1或k2-(a2-1)k+1]=0。① 对于①,当1<a< 11.解 设焦点为F1,F2,椭圆上任一点为P(x0,y0),∠F1PF2=θ,根据余弦定理得 |F1F2|2=|PF1|2+|PF2|2-2|PF1|?|PF2|cosθ, 又|PF1|+|PF2|=2a,则4c2=(2a)2-2|PF1|?|PF2|(1+cosθ),再将|PF1|=a+ex0,|PF2|=a-ex0及a2=b2+c2代入得4b2=2(a2-e2 于是有 由0 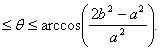 当2b2>a2即 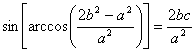 ;当2b2≤a2时,arccos ;当2b2≤a2时,arccos12.解 设A(x1,y1),B(x2,y2),若AB斜率不为0,设为k,直线AB方程为y=k(x+c),代入椭圆方程并化简得 (b2+a2k2)x2+2a2k2cx+a2 (k2c2-b2)=0. ① 则x1,x2为方程①的两根,由韦达定理得 因为y1y2=k2(x1+c)(x2+c),再由②,③得 所以 若斜率不存在,问题等价于 13.解 (1)由双曲线方程得 把①代入C1方程得 Δ=64a2>0,所以方程②必有两个不同实根,设为x1,x2,由韦达定理得x1x2=-a2<0,所以②必有一个负根设为x1,把x1代入①得y2= (2)设过F1( 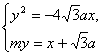 得y2+4 得y2+4联赛一试水平训练题 1.m>5.由已知得 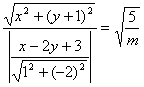 ,说明(x,y)到定点(0,-1)与到定直线x-2y+3=0的距离比为常数 ,说明(x,y)到定点(0,-1)与到定直线x-2y+3=0的距离比为常数2. 3. 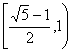 。设点P坐标为(r1cosθ,r1sinθ),点Q坐标为(-r2sinθ,r2cosθ),因为P,Q在椭圆上,可得 。设点P坐标为(r1cosθ,r1sinθ),点Q坐标为(-r2sinθ,r2cosθ),因为P,Q在椭圆上,可得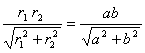 ≤|OF|=c. 所以a2b2≤c2(a2+b2),解得 ≤|OF|=c. 所以a2b2≤c2(a2+b2),解得4.以O为圆心,a为半径的圆。延长F1M交PF2延长线于N,则 5.t∈(0,1]时|AT|min= 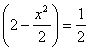 (x-2t)2+2-t2.因为|x|≤2,所以当t∈(0,1]时取x=2t,|AT|取最小值 (x-2t)2+2-t2.因为|x|≤2,所以当t∈(0,1]时取x=2t,|AT|取最小值6. 由①,②得 2x0cosθ=sinθ. ③ 所以 因为l2<1,所以函数f(x)= 所以 7. 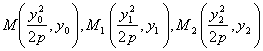 ,由A,M,M1共线得y1= ,由A,M,M1共线得y1=y02(2px-by)+y0?2pb(a-x)+2pa(by-2pa)=0. 当x=a,y= 8. 所以a+b≥ 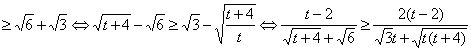 ,又t≤2可得上式成立。 ,又t≤2可得上式成立。9.解 设A(2cosθ, 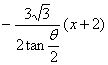 ,同理得 ,同理得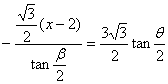 ?(x-2). ?(x-2).两直线方程联立,得P点坐标为 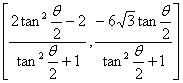 ,消去 ,消去10.解 (1)由  消去y得x2+2a2x+2a2m-a2=0,①设f(x)=x2+2a2x+2a2m-a2,问题(1)转化为方程①在x∈(-a,a)上有唯一解或等根。只需讨论以下三种情况: 消去y得x2+2a2x+2a2m-a2=0,①设f(x)=x2+2a2x+2a2m-a2,问题(1)转化为方程①在x∈(-a,a)上有唯一解或等根。只需讨论以下三种情况:10.Δ=0,得 (2)ΔOAP的面积  时取值最大,此时 时取值最大,此时11.解:设A,B关于l的对称点分别为A1(x2,y2),B1(x1,y1),则AA1中点  在l上, 在l上,所以 y2=k(x2-1) ① 又l 由①,②得  同理,由BB1中点  在l上,且l 在l上,且l 设抛物线方程为y2=2px,将A1,B1坐标代入并消去p得k2-k-1=0. 所以 所以直线l的方程为 联赛二试水平训练题 1.以A为原点,直线AC为x轴,建立直角坐标系,设C(c,0),F(f,0),D(xD,kxD),B(xB,-kxB),则直线DF的方程为 直线BC的方程为 c×①-f×②得 (c-f)x+  ③ ③③表示一条直线,它过原点,也过DF与BC的交点G,因而③就是直线AG的方程。 同理 ,直线AE的方程为 (c-f)x+  ④ ④③,④的斜率互为相反数,所以∠GAC=∠EAC。 2.证明 假设这样的闭折线存在,不妨设坐标原点是其中一个顶点,记它为A0,其他顶点坐标为:  ,…, ,…, ,其中 ,其中bk≡1,dk≡1(k=1,2,…,n),ak+ck≠ak-1+ck-1(k=1,2,…,n,n+1)。 当k=1时,由  ,得 ,得因此b1=±d1,从而 设结论对k=1,2,…,m-1≤n都成立,令 这里 同理可知dm≡1,又am≡abm-1+bam-1(同理cm≡cdm-1+dcm-1). 因此(am+cm-am-1-cm-1)≡(abm-1+bam-1+cdm-1+dcm-1-am-1-cm-1)≡am-1(b-1)+abm-1+cm-1(d-1)+cdm-1≡a+c≡1. 所以am+cm≠am-1+cm-1,结论成立,于是在顶点数n+1为奇数时,an+1+cn+1≠a0+c0,故折线不可能是闭的。 3.证明 (1)由已知B0P0=B0Q0,并由圆弧P0Q0和Q0P0,Q0P1和P1Q1,P1Q1和Q1P1分别相内切于点Q0,P1,Q1,得C1B0+B0Q0=C1P1,B1C1+C1P1=B1C0+C0Q1以及C0Q1=C0B0+ (2)现分别过点P0和P1引上述相应相切圆弧的公切线P0T和P1T交于点T。又过点Q1引相应相切圆弧的公切线R1S1,分别交P0T和P1T于点R1和S1,连接P0Q1和P1Q1,得等腰ΔP0Q1R1和ΔP1Q1S1,由此得∠P0Q1P1=π-∠P0Q1P1-∠P1Q1S1=π-(∠P1P0T-∠Q1P0P)-(∠P0P1T-∠Q1P1P0),而π-∠P0Q1P1=∠Q1P0P1+∠Q1P1P0,代入上式后,即得∠P0Q1P1=π- 同理得∠P0Q0P1=π- 4.证明 引理:抛物线y=ax2+bx+c(a≠0)在(x0,y0)处的切线斜率是2ax0+b. 引理的证明:设(x0,y0)处的切线方程为y-y0=k(x-x0),代入抛物线方程得 ax2+(b-k)x+c+kx0-y0=0. ① 又 故①可化简成 (x-x0)[a(x+x0)+b-k]=0, ② 因为②只有一个实根,所以k=2ax0+b.引理得证。 设P(x0,y0)为任一正交点,则它是由线y=x?tan 又由题设k1k2=-1,所以  ③ ③又因为P(x0,y0)在两条抛物线上,所以  (※) (※)又因为tanα1,tanα2是方程 tanα1+tanα2= tanα1?tanα2= 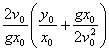 。 ⑤ 。 ⑤把④,⑤代入(※)式得 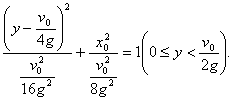 5.证明 以C为原点,CB所在直线为x轴,建立直角坐标系,设∠ADC=θ,|PD|=r.各点坐标分别为D(x1,0),E(0,x1),A(0,x1tanθ),B(x0,0),P(x1-rcosθ,rsinθ). 则lAB方程为 又因为点P在圆上,所以(rcos 要证DP=AP+AE 又因为 因为 所以 (x1-rcosθ)(x1-rcosθ-x0)+r2sin2θ=0. ④ 把②代入④化简得 由①得x0=x1? 代入⑤并约去x1,化简得4sin22 所以sin 6.证明 设BC=d,CD=b,BD=c,则AC=CQ= 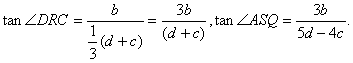 因为0<∠DRC< 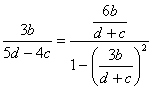 ,化简得9d2-9c2-9b2=0即d2=b2+c2,显然成立。所以命题得证。 ,化简得9d2-9c2-9b2=0即d2=b2+c2,显然成立。所以命题得证。本系列讲座由在人教中数论坛网友“0.1”整理提供,感谢他(她)的分享。 (责任编辑:admin) |
