|
第三章《概率》复习测试题（二） 三、解答题 12.(2011·福建文)某日用品按行业质量标准分成五个等级，等级系数  依次为1，2，3，4，5．现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：
⑴若所抽取的20件日用品中，等级系数为4的恰有3件，等级系数为5的恰有2件，求  的值；⑵在⑴的条件下，将等级系数为4的3件日用品记为  ，等级系数为5的2件日用品记为 ，现从，，这5件日用品中任取两件(假定每件日用品被取出的可能性相同)，写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率.考查目的：考查概率统计有关知识，函数方程和分类整合思想，以及数据处理和运算求解能力等. 答案：⑴  ；⑵0.4.解析：⑴由频率分布表得  即 .∵抽取的20件日用品中，等级系数为4的恰有3件，∴ .等级系数为5的恰有2件，∴ ，从而 ，∴.⑵从日用品 ，中任取两件，所有可能的结果为 ， ， ， ， ， ， ， ， ， .设事件A表示“从日用品，中任取两件，其等级系数相等”，则A包含的基本事件为，，，共4个，又∵基本事件的总数为10，∴所求的概率 .13.口袋中有质地、大小完全相同的5个球，编号分别为1，2，3，4，5.甲先摸出一个球，记下编号为  ，放回袋中后，乙再摸一个球，记下编号为 .⑴求“  ”事件发生的概率；⑵若点  落在圆 内，则甲赢，否则算乙赢，这个游戏规则公平吗？试说明理由.考查目的：本题主要考查用列举法计算随机事件所含的基本事件数及事件发生的概率等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力. 答案：⑴  ；⑵对乙不公平.解析：⑴设“ ”为事件A，其包含的基本事件为(1，5)，(2，4)，(3，3)，(4，2)，(5，1)共5个，又∵基本事件总数有5×5＝25(个)，∴ .⑵这个游戏规则不公平.设甲胜为事件B，则其所包含的基本事件为(1，1)，(1，2)，(1，3)，(1，4)，(2，1)，(2，2)，(2，3)，(2，4)，(3，1)，(3，2)，(3，3)，(4，1)，(4，2)共13个，∴  ，故而对乙不公平.14.(2010·湖南文)为了对某课题进行研究，用分层抽样方法从三所高校A，B，C的相关人员中，抽取若干人组成研究小组、有关数据见下表(单位：人)
⑴求  ；⑵若从高校B、C抽取的人中选2人作专题发言，求这二人都来自高校C的概率. 考查目的：巩固分层抽样的知识，列举法求随机事件包含的基本事件数. 答案：⑴  ；⑵ .解析：⑴由题意得  ，∴；⑵记从高校B抽取的2人为 ，从高校C抽取的3人为 ，则从高校B，C抽取的5人中选2人作专题发言的基本事件有 ， 共10种.设选中的2人都来自高校C的事件为，则包含的基本事件有 共3种，∴ ，∴选中的2人都来自高校C的概率为.15.(2010·陕西文)为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行抽样检查，测得身高情况的统计图如下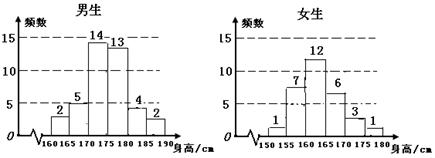：  ⑴估计该校男生的人数； ⑵估计该校学生身高在170～185cm之间的概率； ⑶从样本中身高在180～190cm之间的男生中任选2人，求至少有1人身高在185～190cm之间的概率. 考查目的：本题考查频数，频率及概率，频率与概率的关系，考查运用统计知识解决简单实际问题的能力，数据处理能力和运用意识. 答案：⑴400；⑵0.5；⑶  .解析：⑴样本中男生人数为40，由分层出样比例为10%估计全校男生人数为400. ⑵有统计图知，样本中身高在170～185cm之间的学生有14+13+4+3+1=35人，样本容量为70 ，所以样本中学生身高在170～185cm之间的频率  ，故由 估计该校学生身高在170～180cm之间的概率 .⑶样本中身高在180～185cm之间的男生有4人，设其编号为①，②，③，④，样本中身高在185～190cm之间的男生有2人，设其编号为⑤，⑥，从上述6人中任取2人的树状图为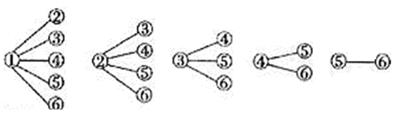：  故从样本中身高在180～190cm之间的男生中任选2人得所有可能结果数为15，至少有1人身高在185～190cm之间的可能结果数为9，∴所求概率  .(责任编辑：admin) |
