第二章《统计》测试题(一)
一、选择题
1. 为了了解所加工一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( ). 为了了解所加工一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( ).
A.总体 B.个体是每一个零件 C.总体的一个样本 D.样本容量
考查目的:考查总体、样本、校本的容量等概念.
答案:C.
解析:200个零件的长度是总体的一个样本.
|
一年级
|
二年 级 级
|
三年级
|
女生
|
373
|
|

|
男生
|
377
|
370
|
z
|
2.某校共有学生2 000名,各年级男、女生人数如下表.已知在全校学生中随 机抽取1名,抽到二年级女生的频率是0.19 机抽取1名,抽到二年级女生的频率是0.19 .现用分层抽样的方法在全校抽取64名学生,则在三年级应抽取学生的人数为( ). .现用分层抽样的方法在全校抽取64名学生,则在三年级应抽取学生的人数为( ).

A.24 B.18 C.16 D.12
考查目的:考查分层抽样的概念与方法.
答案:C.
解析:设二年级女生的人数为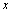 ,则由 ,则由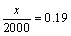 ,得 ,得 , , 即二年级的女生有380人,那么三年级的学生的人数应该是2000-373-377-380-370=500,即总体中各个年级的人数比例为3∶3∶2,故在分层抽样中应在三年级抽取的学生人数为 即二年级的女生有380人,那么三年级的学生的人数应该是2000-373-377-380-370=500,即总体中各个年级的人数比例为3∶3∶2,故在分层抽样中应在三年级抽取的学生人数为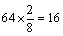 . .
3.右图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学 生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中 生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中 可以得到这10位同学身高的中位数是( ) 可以得到这10位同学身高的中位数是( )

A.161cm B.162cm C.163cm D.164cm
考查目的:考查茎叶图的识读与众数、中位数、平均数等数字特征的计算与辨别.
答案: B.
解析:由给定的茎叶图可知,这10位同学身高的中位数为 (cm). (cm).
4.对某种电子元件的使用寿命进行跟踪调查,所得样本的频率分布直方图如图所示,由图可知,这一批电子元件中使用寿命在100~300 h的电子元件的数量与使用寿命在3 00~600 h的电子元件的数量的比是( ). 00~600 h的电子元件的数量的比是( ).

A.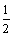 B. B. C. C. D. D.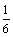
考查目的:考查频率分布直方图的识读与应用.
答案:C.
解析:寿命在100~300 h的电子元件的频率为 ;寿命在300~600 h的电子元件的频率为 ;寿命在300~600 h的电子元件的频率为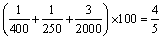 ,∴它们的电子元件数量之比为 ,∴它们的电子元件数量之比为 . .
5.(2012山东文)在某次测 量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两个样本的下列数字特征相同的是( ). 量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两个样本的下列数字特征相同的是( ).
A.众数 B.平均数 C.中位数 D.标准差
考查目的:考查众数、平均数、中位数、标准差的意义与计算.
答案:D.
解析:设A样本的数据为变量为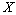 ,B样本的数据为变量为 ,B样本的数据为变量为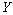 , , 则满足 则满足 ,因为A样本的众数、平均数、中位数分别是88、86、86,所以B样本的众数、平均数、中位数分别是90、88、88,而A样本的标准差 ,因为A样本的众数、平均数、中位数分别是88、86、86,所以B样本的众数、平均数、中位数分别是90、88、88,而A样本的标准差 =2,B样本的标准差 =2,B样本的标准差
 ,∴A,B两个样本的标准差相等. ,∴A,B两个样本的标准差相等.
6.(2011陕西改编)设( , , ),( ),(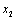 , ,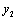 ),…,( ),…,( , ,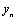 )是变量 )是变量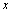 和 和 的n个样本点,直线 的n个样本点,直线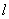 是由这些样本点通过最小二乘法得到的线性回归直线如图所示,则以下结论正确的是( ). 是由这些样本点通过最小二乘法得到的线性回归直线如图所示,则以下结论正确的是( ).
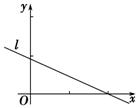
A.变量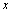 和 和 之间呈现正相关关系 之间呈现正相关关系
B.各样本点( , , )到直线 )到直线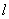 的距离都相等 的距离都相等
C.当n为偶数时,分布在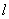 两侧的样本点的个数一定相同 两侧的样本点的个数一定相同
D.直线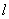 过点 过点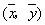
考查目的:考查用回归分析法求线性回归方程的相关知识.
答案:D.
解析:由图可知,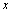 和 和 之间是负相关关系,故A错;由最小二乘法原理可知,各样本点到直线 之间是负相关关系,故A错;由最小二乘法原理可知,各样本点到直线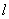 的距离的和最小,故B错;回归直线 的距离的和最小,故B错;回归直线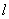 与分布在两侧的样本点的个数无关,故C错;由样本的中心 与分布在两侧的样本点的个数无关,故C错;由样本的中心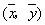 落在回归直线 落在回归直线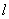 上可知,D正确. 上可知,D正确.
二、填空题
7.若在体育彩票000001~100000编号中,凡彩票号码最后三位数为345的即为一等奖,则这里采用的抽样方法是 .
考查目的:考查系统抽样的意义和基本特征.
答案:系统抽样.
解析:依题意,号码为000345、001345、…、099345的彩票均为一等奖,该抽样符合系统抽样的特点,分段间隔为1000.
8.(2010安徽文)某地有居民100000户,其中普通家庭99000户,高收入家庭1000户.从普通家庭中以简单随机抽样方式抽取990户,从高收入家庭中以简单随机抽样方式抽取l00户进行调查,发现共有120户家庭拥有3套或3套以上住房,其中普通家庭50户,高收人家庭70户.依据这些数据并结合所掌握的统计知识,你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是 .
考查目的:考查分层抽样的意义和基本方法,体会用样本估计总体的简单应用.
答案:5.7%.
解析:本题分层抽样问题,首先根据拥有3套或3套以上住房的家庭所占的比例,得出100 000户,居民中拥有3套或3套以上住房的户数,它除以100 000得到的值,为该地拥有3套或3套以上住房的家庭所占比例的合理估计.该地拥有3套或3套以上住房的家庭可以估计有 户,所以所占比例的合理估计是 户,所以所占比例的合理估计是 . .
9.在如图所示的茎叶图中,甲 、乙两组数据的中位数分别是 、 . 、乙两组数据的中位数分别是 、 .

考查目的:考查茎叶图的识读与样本特征数字的辨别.
答案:45、46.
解析:由茎叶图可知,甲图中共有9个数,分别为28,31,39,45,42,55,58,57,66,其中位数为45;乙图中共有9个数分别为29,34,35,48,42,46,53,55,67其中位数为46.
10.(2011浙江)某中学为了解学生数学课程的学习情况,在3 000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3 000名学生在该次数学考试中成绩小于60分的学生数是 .
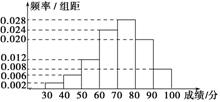
考查目的:考查频率分布直方图的识读与理解,体会频率分布直方图的意义和作用.
答案:600.
解析:根据样本的频率分布直方图,成绩小于60分的学生的频率为(0.002+0.006+0.012)×10=0.20,所以可推测3 000名学生中成绩小于60分的人数为3000×0.20=600.
11.某人5次上班途中所花的时间(单位:分钟)分别为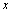 , , ,10,11,9.已知这组数据的平均数为10,方差为2,则 ,10,11,9.已知这组数据的平均数为10,方差为2,则 的值 的值 为 . 为 .
考查目的:考查平均数、方差的意义与应用.
答案: 208.
解析: 由 , ,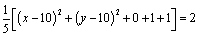 ,联立解得 ,联立解得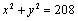 . .
(责任编辑:admin) |





