|
南昌市高中新课程训练题（直线和圆的方程） 命题人：南昌八中 骆 敏 一、 选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。 1.在直角坐标系中，直线  的倾斜角是（ ）A．  B． C． D． 2.直线l经过A（2，1）、B（1，m2）(m∈R)两点，那么直线l的倾斜角的取值范围是（ ） A．  B． C． D． 3. 直线  同时要经过第一、第二、第四象限，则 应满足（ ）A．  B． C． D． 4.已知点A（6，－4），B（1，2）、C（x,y）,O为坐标原点。若  则点C的轨迹方程是( )A．2x－y+16＝0 B．x－y－10＝0 C．x－y+10＝0 D．2x－y－16＝0 5. 由动点Ｐ向圆x2 + y2=1引两条切线PA、PB,切点分别为A、B，∠APB=60°,则动点Ｐ的轨迹方程为 ( ) A x2+y2=4 B x2+y2=3 C x2+y2=2 D x2+y2=1 6. 已知直线  的方程为 ，直线 的方程为 （ 为实数）．当直线 与直线 的夹角在（0， ）之间变动时，的取值范围是 （ ）A.（  ，1）∪（1， ） B.（ ， ） C.（0，1） D.（1， ）7.若点（5，b）在两条平行直线6x－8y+1=0与3x－4y+5=0之间，则整数b的值为 ( ) A．5 B．－5 C．4 D．－4 8．不等式组  表示的平面区域是 （ ）A．矩形 B．三角形 C．直角梯形 D．等腰梯形 9．已知直线  与圆 相切，则三条边长分别为 的三角形是（ ）A．锐角三角形 B．直角三角形 C．钝角三角形 D．不存在 10．已知圆x2+y2+2x-6y+F=0与x+2y-5=0交于A, B两点, O为坐标原点, 若OA⊥OB, 则F的值为 ( ) A -1 B 0 C 1 D 2 11．已知圆  ，点 （－2，0）及点 （2，），从点观察点，要使视线不被圆 挡住，则的取值范围是A.（－∞，－1）∪（－1，+∞） B.（－∞，－2）∪（2，+∞） C.（－∞，  ）∪（ ，+∞） D.（－∞，－4）∪（4，+∞）12．在圆x2+y2＝5x内，过点  有n条弦的长度成等差数列，最小弦长为数列的首项a1，最大弦长为an，若公差 ，那么n的取值集合为 （ ）A．{4，5，6，7} B．{4，5，6} C．{3，4，5，6} D． {3，4，5} 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。 13．半径为5的圆过点A(－2, 6)，且以M(5, 4)为中点的弦长为2  ，则此圆的方程是 。14．过点  (1，2)的直线l将圆 分成两段弧，其中的劣弧最短时，l的方程为 ．15．已知圆  与 轴交于 两点，与 轴的另一个交点为 ，则 ．16．已知圆的方程是x2＋y2＝1，则在y轴上截距为  且与圆相切的直线方程为 。三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。 17．已知点A(2, 0), B(0, 6), O为坐标原点. (1)若点C在线段OB上, 且∠BAC=45°, 求△ABC的面积;(2) 若原点O关于直线AB的对称点为D, 延长BD到P, 且|PD|=2|BD|.已知直线l:ax+10y+84-108  =0经过P, 求直线l的倾斜角。18．圆的方程为x2+y2－6x－8y＝0，过坐标原点作长为8的弦，求弦所在的直线方程。 19．已知定点A(0,1)，B(0,－1)，C(1,0)。动点P满足：  。(1)求动点P的轨迹方程，并说明方程表示的曲线；(2)当  的最大值和最小值。 20．已知圆M：2x2+2y2－8x－8y－1＝0和直线l：x+y－9＝0过直线 上一点A作△ABC，使∠BAC=45°，AB过圆心M，且B，C在圆M上。 ⑴当A的横坐标为4时，求直线AC的方程；⑵求点A的横坐标的取值范围。 21．已知圆C：  ，是否存在斜率为1的直线l，使l被圆C截得的弦AB为直径的圆过原点，若存在求出直线l的方程，若不存在说明理由。22．某建筑物内一个水平直角型过道如图所示，两过道的宽度均为3米，有一个水平截面为矩形的设备需要水平移进直角型过道，若该设备水平截面矩形的宽为1米，长为7米. 问：该设备能否水平移进拐角过道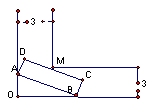？  参考答案 一、1．C 2．D 3．A 4．D 5．B 6．A 7．B 8．B 9．C 10．B 11．C 12．A 二、13．(x－1)2＋(y－2)2＝25或(x－  )2＋(y－ )2＝25 14． 15． 16． 三、17．解：(1)依条件易知kAB=-3. 由tan45°=  ,得kAC= - .∴直线AC: y=-(x-2).令x=0,得y=1,则C(0, 1). ∴S△ABC= |BC||OA|=5. (2)设D点的坐标为(x0, y0),∵直线AB:  即3x+6y-6=0, ∴  . 解得x0= y0= . 由|PD|=2|BD|, 得λ=  . ∴由定比分点公式得xp= .将P(  )代入l的方程, 得a=10. ∴k1= -. 故得直线l的倾斜角为120°18．解：x2+y2－6x－8y=0即(x－3)2+(y－4)2=25，设所求直线为y＝kx。 ∵圆半径为5，圆心M（3，4）到该直线距离为3， ∴  ，∴  ，∴ 。 ∴所求直线为y 或 。19．解：(1)设动点的坐标为P(x,y),则  ＝(x,y－1)， ＝(x,y+1)， ＝(1－x,－y)∵ ·＝k||2，∴x2+y2－1＝k[(x－1)2+y2] 即(1－k)x2+(1－k)y2+2kx－k－1=0。若k=1，则方程为x=1，表示过点（1，0）是平行于y轴的直线。 若k≠1，则方程化为：  ，表示以(－  ,0)为圆心，以 为半径的圆。(2)当k=2时，方程化为(x－2)2+y2=1。∵2 ＋＝2(x,y－1)＋(x,y+1)＝(3x,3y－1)，∴|2 ＋|＝ 。又x2+y2＝4x－3，∴|2 ＋|＝ ∵(x－2)2+y2＝1，∴令x＝2＋cosθ，y＝sinθ。则36x－6y－26＝36cosθ－6sinθ+46＝6  cos(θ+φ)+46∈[46－6,46＋6]，∴|2 ＋|max＝ ＝3＋，|2＋|min＝ ＝-3。20．解：⑴依题意M（2，2），A（4，5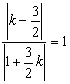），  ，设直线AC的斜率为 ，则 ,解得 或 ，故所求直线AC的方程为5x+y－25＝0或x－5y+21＝0；⑵圆的方程可化为(x－2)2+(y－2)2＝  ，设A点的横坐标为a。则纵坐标为9－a；① 当a≠2时，  ，设AC的斜率为k，把∠BAC看作AB到AC的角，则可得  ，直线AC的方程为y－(9－a)＝ (x－a)即5x－(2a－9)y－2a2+22a－81＝0， 又点C在圆M上，所以只需圆心到AC的距离小于等于圆的半径，即 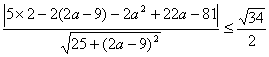 ，化简得a2－9a+18≤0，解得3≤a≤6；②当a＝2时，则A（2，7）与直线 x=2成45°角的直线为y－7＝x－2即x－y+5＝0， M到它的距离  ，这样点C不在圆M上，还有x+y－9＝0，显然也不满足条件，故A点的横坐标范围为［3，6］。21．解：圆C化成标准方程为  假设存在以AB为直径的圆M，圆心M的坐标为（a，b） 由于CM⊥ l，∴kCM×kl= -1 ∴kCM=  ， 即a+b+1=0，得b= -a-1 ①直线l的方程为y-b=x-a，即x-y+b-a=0 CM=  ∵以AB为直径的圆M过原点，∴   ， ∴ ②把①代入②得  ，∴ 当  此时直线l的方程为x-y-4=0；当  此时直线l的方程为x-y+1=0故这样的直线l是存在的，方程为x-y-4=0 或x-y+1=0 22．解：由题设，我们以直线OB,OA分别为x轴，y轴建立直角坐标系，问题可转化为：求以M(3,3)点为圆心，半径为1的圆的切线被x的正半轴和y的正半轴所截的线段 AB长的最小值。设直线AB的方程为  ，∵它与圆 相切，
 ∴  ……（1） ，又∵原点O(0,0)与点M(3,3)在直线 的异侧，∴  ，∴（1）式可化为  ……（2）下面求  （a>0,b>0）的最小值。设  代入（2）得 ，…（3） 再设t=sinθ+cosθ,  . ,代入（3）得  ， ,记 这里f(1)=－4<0, 在 内有解  。这时 这说明能水平移过的宽1米的矩形的长至多为  ，故该设备不能水平移进过道。 另解：  ∴r(t) 在 上是减函数， 。(责任编辑：admin) |
