|
怎样通过“折叠问题”来提高自己的空间想象能力和巩固相关的立体几何知识? 一般地说,这里的问题常常是把一个已知的平面图形折叠成一个立体图形(相反的问题是“展平问题”,即把一个已知的立体图形展开一个平面图形)。这里要求我们认清平面图形中各已知条件的相互关系及其本质,并且在把这一平面图形折叠成立体图形以后,能分清已知条件中有哪些发生了变化,哪些未发生变化。这些未变化的已知条件都是我们分析问题和解决问题的依据。教科书第47页上的第13,14题,也是折叠问题,又如选择题: 如下面左图,在正方形SG1G2G3中,E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个由四个三角形围成的“四面体”,使G1、G2、G3三点重合,重合后的点记为G(下面右图)。那么在四面体S-EFG中必有 (A)SG⊥ΔEFG所在平面 (B)SD⊥ΔEFG所在平面 (C)GF⊥ΔSEF所在平面 (D)GD⊥ΔSEF所在平面 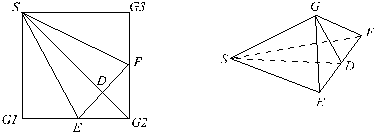 这道题虽然涉及“四面体”的概念,实际上主要用来巩固直线和平面垂直的判定定理和培养我们的空间想象能力。已知的是一个正方形,那么SG1⊥G1E,EG2⊥G2F,FG3⊥G3S,G3S⊥SG1,这些条件在折叠后仍然不变。这一点就是我们解决问题的主要思路。 根据这一点,可以看出,折叠后得到的四面体S-EFG中,一定有SG⊥GE,SG⊥GF,即SG⊥ΔEFG所在平面。于是应该选A。 (责任编辑:admin) |
