|
随着指数范围的扩充,幂的运算性质是否可以合并并简化? 正整数指数幂的运算性质如下: (1)am·an=am+n (m,n∈Z+) ; (2)(am)n=amn (m,n∈Z+); (3)(ab)n=anbn (n∈Z+) ; (4)am÷an=am-n (a≠0,m,n∈Z+,且m>n); (5) 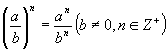 当指数的范围扩大到整数集Z后,幂的运算性质可由5条合并为3条,即:(1)' am·an=am+n (m,n∈Z) ;(2)' (am)n=amn (m,n∈Z);(3)' (ab)n=anbn (n∈Z) 。不过,这3条性质都要遵守零指数幂、负整指数幂的底数不能等于0的规定。 当指数的范围扩大到有理数集Q以至实数集R后,幂的运算性质仍然是上述(1)'、(2)'、(3)'这3条,当然,这3条性质也要遵守负实数指数幂的底数不能等于0的规定。 (责任编辑:admin) |
