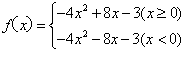|
西城教育研修学院中学数学室供稿 高一年级数学期中练习试卷（卷1） 一、选择题（本大题共8小题，每小题5分，共40分，将正确答案的序号填在机读卡上） 1、设集合  ， ，则下列关系中正确的是(A)  (B)  (C)  (D)  2、已知全集  则 (A) {5} (B) {2，6} (C) {2，3，4，6} (D) {3} 3、  ，则使函数 的定义域为R且为奇函数的所有 的值为(A) 1,3 (B) -1,1 (C) -1,3 (D) -1,1,3 4、与函数 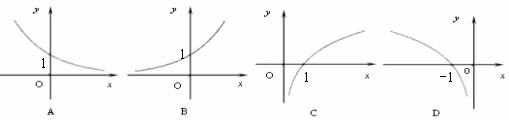 的图象关于 轴对称的函数图象是 5、已知函数  为 上的减函数，则满足 的实数 的取值范围是(A)  (B)  (C)  (D)  6、为了得到函数  的图象，只需把函数上所有点 (A)向右平移3个单位长度，再向下平移1个单位长度 (B)向左平移3个单位长度，再向下平移1个单位长度 (C)向右平移3个单位长度，再向上平移1个单位长度 (D)向左平移3个单位长度，再向上平移1个单位长度 7、设P、Q为两个非空实数集合，定义集合   ，则 中元素的个数是 (A)9 (B) 8 (C)7 (D)6 8、在  这四个函数中，当 时，使 恒成立的函数的个数是(A) 0 (B) 1 (C) 2 (D) 3 二、填空题（本大题共4小题，每小题5分，共20分，将正确答案填在答题纸上） 9、设函数  为奇函数，则实数 。10、设  ， ， ，若 ，则 由小到大的排列是。 11、若  ， ，则 ； 。12、函数  的单调递增区间是 。三、解答题（本大题共3小题，共40分，请将必要的解答过程写在答题纸上） 13、（本题满分13分） 设函数  满足：对任意 都有 ，且 （1）求  的值；（2）求   的值；（3）判断函数  是否具有奇偶性，并证明你的结论。14、（本题满分13分） 定义在实数R上的函数 是偶函数，当x≥0时， .（Ⅰ）求f（x）在R上的表达式； （Ⅱ）求y=f（x）的最大值，并写出  在R上的单调区间（不必证明）。15、（本题满分14分） 已知函数  是奇函数，且 。（1）求函数 的解析式；（2）求证：  ；（3）判断函数f(x)在  上的单调性，并加以证明。高一年级数学期中练习试卷（卷2） 四、填空题（本大题共2小题，每小题5分，共10分，将正确答案填在答题纸上） 16、设f(x)是定义在R上的奇函数，且y=f (x)的图象关于直线  对称，则f (1)+ f (2)+ f (3)+ f (4)+ f (5)=_______________。 17、已知  ，则不等式 的解集为 。五、解答题（本大题共3小题，共40分，写出必要的解答过程） 18、（本题满分13分） 已知函数 已知二次函数
（1） 若方程 （2） 若 |
， 
大致图像；
的值；
时，求
。若A城的供电量为20亿度/月，B城供电量为10亿度/月。
，且不等式
的解集为
。
有两个相等的实根，求
，10 
, 11 
12 
；（2）
， 单调增区间
单调减区间
(3)
元
