西城教育研修学院中学数学室供稿
班级 学号 姓名 成绩
一、 选择题(本题共15道小题,每题4分,总分60分,每小题只有一个正确答案,将答案填入题后括号中)
1.已知A={1,a},则下列不正确的是( )
A.a∈A B.1∈A C.(1,a)∈A D.1≠a
2.若点(x,y)在映射 下的象是点(x+y,x-y),则在映射 下的象是点(x+y,x-y),则在映射 下点(2,1)的象是( ) 下点(2,1)的象是( )
A.(3,1) B.  C. C. 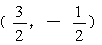 D.(1,3) D.(1,3)
3.函数 的定义域( ) 的定义域( )
A.  B. B. 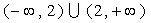 C. C. 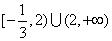  D. D. 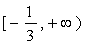
4.设x取实数,则f(x)与g(x)表示同一个函数的 ( )
A.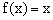 , ,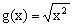 B. B. , ,
C.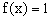 , , D. D. , ,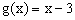
5.若函数 的图象过点 的图象过点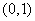 ,则b等于( ) ,则b等于( )
A.2 B.-2 C.1 D.-1
6.已知 ,那么 ,那么 用 用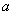 表示是( ) 表示是( )
A.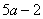 B. B.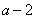 C. C.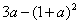 D. D. 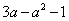
7.若函数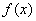 为偶函数,当 为偶函数,当 时, 时,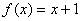 ,则 ,则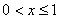 , ,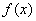
的解析式为( )
A. B. B.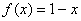
C.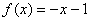 D. D.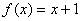
8. 下列函数中是奇函数的是( )
A.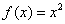 B. B. 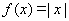 C. C. D. D.
9.在同一坐标系中,函数y = 与 与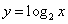 的图象之间的关系是( ) 的图象之间的关系是( )
A.关于y轴对称 ..B.关于x轴对称
C.关于原点对称 D.关于直线y = x对称
10.在区间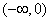 上为增函数的是( ) 上为增函数的是( )
A. 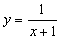 B. B. 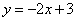 C. C. 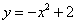 D. D. 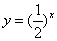
11.三个数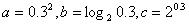 之间的大小关系是( ) 之间的大小关系是( )
A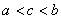 B. B.  C. C. 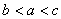 D. D.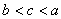
12.已知定义在R上函数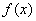 的图象是连续不断的,且 的图象是连续不断的,且 , ,
那么函数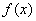 一定存在零点的区间是( ) 一定存在零点的区间是( )
A.(2,2.5) B.(2.5,3) C.(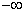 ,2) D.以上都不对 ,2) D.以上都不对
13.设函数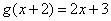 ,则 ,则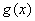 的表达式是( ) 的表达式是( )
A.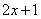 B. B. C. C. D. D.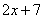
14.当 时,在同一坐标系中,函数 时,在同一坐标系中,函数 的图象是( ) 的图象是( )
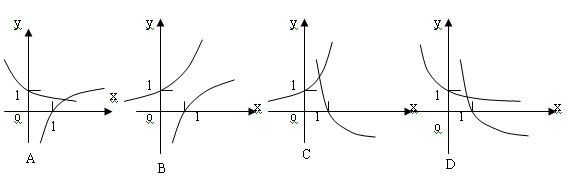
15.直角梯形OABC中AB∥OC、AB=1、OC=BC=2, 直线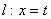 截该梯形所得位于 截该梯形所得位于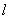 左边图形面积为S,则函数S= 左边图形面积为S,则函数S=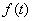 的图像大致为( ) 的图像大致为( )
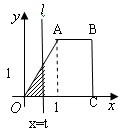
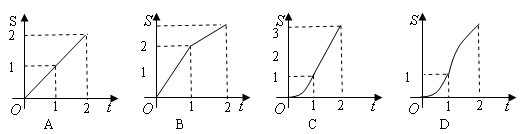
二、填空题(共5小题,每题4分,共20分)
16.已知全集U=R,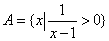 , ,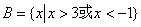 , ,
则  = , = ,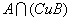 = =
17.函数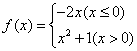 ,则 ,则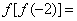 ;若 ;若 ,则x= ,则x=
18. 为了得到函数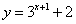 的图象,只需把函数 的图象,只需把函数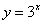 的图象上的所有点 的图象上的所有点
向 平移 个单位长度,再向 平移 个单位长度。
19.已知函数 ,对任意 ,对任意 时, 时,
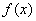 的函数值恒为负,则 的函数值恒为负,则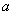 的取值范围 的取值范围
20.设奇函数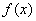 的定义域为 的定义域为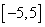 ,若当 ,若当 时, 时, 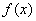 的图象如下图,则不等式 的图象如下图,则不等式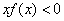 的解集是 的解集是
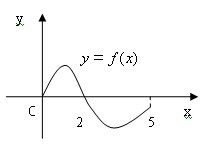
三、解答题(共3小题,共20分)
21、(6分)已知集合 若 若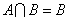 ,求实数 ,求实数 的取值范围。 的取值范围。
22、(6分)已知二次函数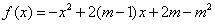
(1)如果它的图象经过原点,并且在区间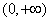 上是单调递减函数,求实数 上是单调递减函数,求实数 的值; 的值;
(2)如果它的图象关于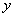 轴对称,求 轴对称,求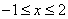 时,函数 时,函数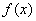 的值域。 的值域。
23、(8分)已知函数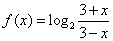
(1) 求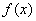 的定义域 的定义域
(2) 判断函数的奇偶性,并给以证明
(3) 判断并用定义证明函数的单调性
四、解答题(共2小题,20分)
24、已知定义在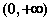 上的函数 上的函数 ,当 ,当 时, 时, ,且对于任意的 ,且对于任意的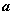 、 、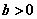 ,有 ,有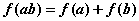
(1) 证明: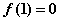
(2) 求证: 在 在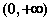 上单调递增 上单调递增
(3)已知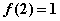 ,且 ,且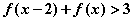 ,试确定 ,试确定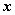 的取值 的取值
25、设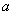 为实数,函数 为实数,函数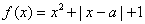 , ,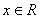
(1)讨论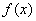 的奇偶性; 的奇偶性;
(2)求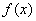 的最小值 的最小值
答案:
一、选择题
CACBA BBDDC CABCC
二、填空题
16.  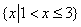
17. 17 -5,3
18. 左1上2 或 上2左1
19. 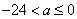
20. 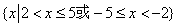 或 或 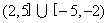
三、解答题
21、(6分)已知集合 若 若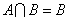 ,求实数 ,求实数 的取值范围。 的取值范围。
解: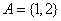

22、(6分)已知二次函数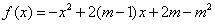
(1)如果它的图象经过原点,并且在区间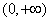 上是单调递减函数,求实数 上是单调递减函数,求实数 的值; 的值;
(2)如果它的图象关于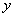 轴对称,求 轴对称,求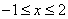 时,函数 时,函数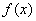 的值域 的值域
解:(1)m=0
(2) 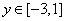
23、(8分)已知函数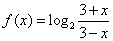
(1)求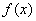 的定义域 的定义域
(2)判断函数的奇偶性,并给以证明
(3)判断并用定义证明函数的单调性
解:(1)  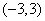
(2)奇函数
(3) 略
四、解答题(共2小题,20分)
24、已知定义在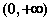 上的函数 上的函数 ,当 ,当 时, 时, ,且对于任意的 ,且对于任意的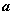 、 、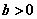 ,有 ,有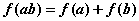
(4) 证明: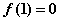
(5) 求证: 在 在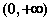 上单调递增 上单调递增
(3)已知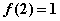 ,且 ,且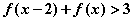 ,试确定 ,试确定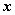 的取值 的取值
解:
(1) 令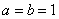 ,∵ ,∵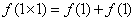 ,∴ ,∴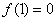
(2) 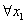 、 、 , , ,则 ,则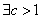 , ,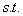 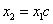
∴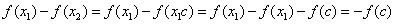
∵ , ,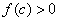
∴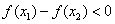
∴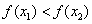
∴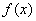 为 为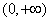 上的增函数 上的增函数
(3) ∵ , ,
∴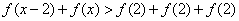
∴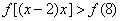
∴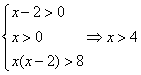
∴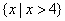
25、设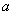 为实数,函数 为实数,函数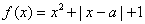 , ,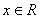
(1)讨论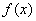 的奇偶性; 的奇偶性;
(2)求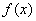 的最小值 的最小值
解:(1)当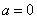 时, 时, 为偶函数, 为偶函数,
当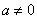 时, 时,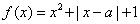 为非奇非偶函数; 为非奇非偶函数;
(2)当 时, 时,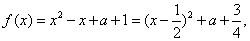
当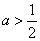 时, 时,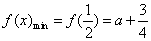 , ,
当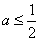 时, 时,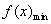 不存在; 不存在;
当 时, 时,
当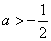 时, 时,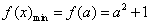 , ,
当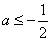 时, 时,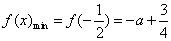
综上所述: 当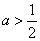 时 时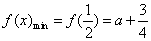 , ,
当 时, 时,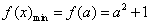
当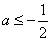 , ,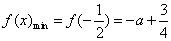
西城外国语模块1测试试卷含答案.zip
(责任编辑:admin) |