|
【考题回放】 1．设 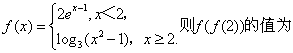 （C ）A.0 B.1 C.2 D.3 2．函数y=f(x)的图象与y=2  的图象关于y轴对称，若y=f-1(x)是y=f(x)的反函数，则y=f-1(x2-2x)的单调增区间是（ D ）A.[1，+∞] B.（2，+∞） C.（-∞，1 ） D.（-∞，0） 3.在下列四个函数中，满足性质：“对于区间(1,2)上的任意x1,x2(x1¹x2)， |f(x1)-f(x2)|<|x2-x1|恒成立”的只有(A ) A.  B. C. D. 4.已知函数  ，若f(x)为奇函数，则 ________。（ ）5.对a,b  R,记max|a,b|= 函数f（x）＝max||x+1|,|x-2||(xR)的最小值是___.（ ）6.对定义域是Df、Dg的函数y=f(x)、y=g(x)，规定：函数  。（1）若函数  ，g(x)=x2，写出函数h(x)的解析式；（2）求问题（1）中函数h(x)的值域； （3）若g(x)= f(x+a)，其中a是常数，且aÎ[0,p]，请设计一个定义域为R的函数y=f(x)，及一个a的值，使得h(x)=cos4x，并予以证明。 【解答】： (1)  (2) 当x≠1时, h(x)=  =x-1+ +2,若x>1时, 则h(x)≥4,其中等号当x=2时成立 若x<1时, 则h(x)≤ 0,其中等号当x=0时成立 ∴函数h(x)的值域是(-∞,0]∪{1}∪[4,+∞) (3)令 f(x)=sin2x+cos2x,α=  则g(x)=f(x+α)= sin2(x+ )+cos2(x+)=cos2x-sin2x,于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x. 另解令f(x)=1+  sin2x, α= ,g(x)=f(x+α)= 1+ sin2(x+π)=1-sin2x,于是h(x)= f(x)·f(x+α)= (1+ sin2x)( 1-sin2x)=cos4x. (责任编辑：admin) |