33、(四川理)设函数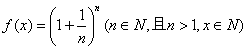 . .
(Ⅰ)当x=6时,求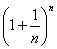 的展开式中二项式系数最大的项; 的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明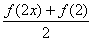 > >
(Ⅲ)是否存在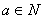 ,使得an< ,使得an<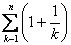 < <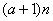 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由. 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
本题考察函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法。考查综合推理论证与分析解决问题的能力及创新意识。
(Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是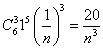
(Ⅱ)证法一:因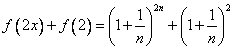
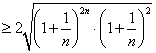  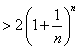
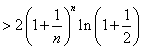 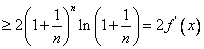
证法二:因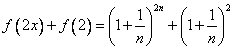 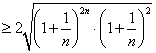 
而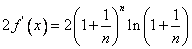
故只需对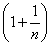 和 和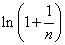 进行比较。 进行比较。
令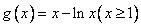 ,有 ,有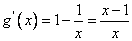
由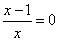 ,得 ,得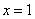
因为当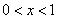 时, 时,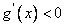 , ,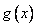 单调递减;当 单调递减;当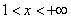 时, 时,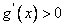 , ,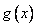 单调递增,所以在 单调递增,所以在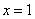 处 处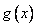 有极小值 有极小值
故当 时, 时,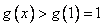 , ,
从而有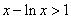 ,亦即 ,亦即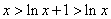
故有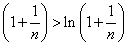 恒成立。 恒成立。
所以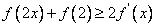 ,原不等式成立。 ,原不等式成立。
(Ⅲ)对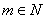 ,且 ,且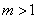
有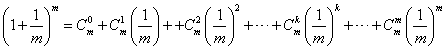
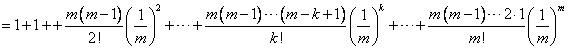
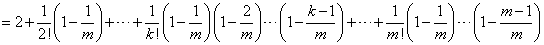
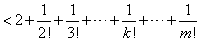

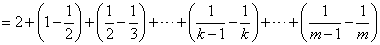
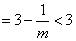
又因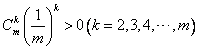 ,故 ,故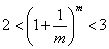
∵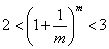 ,从而有 ,从而有 成立, 成立,
即存在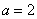 ,使得 ,使得 恒成立。 恒成立。
34、(陕西理)设函数f(x)=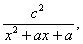 其中a为实数. 其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时,求f(x)的单减区间.
解:(Ⅰ)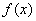 的定义域为 的定义域为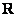 , ,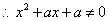 恒成立, 恒成立,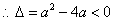 , ,
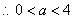 ,即当 ,即当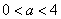 时 时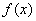 的定义域为 的定义域为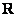 . .
(Ⅱ)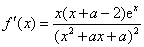 ,令 ,令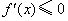 ,得 ,得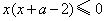 . .
由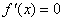 ,得 ,得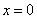 或 或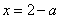 ,又 ,又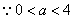 , ,
 时,由 时,由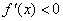 得 得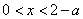 ; ;
当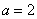 时, 时,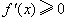 ;当 ;当 时,由 时,由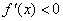 得 得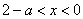 , ,
即当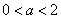 时, 时,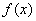 的单调减区间为 的单调减区间为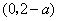 ; ;
当 时, 时,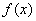 的单调减区间为 的单调减区间为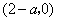 . .
35、(山东理)设函数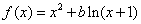 ,其中 ,其中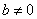 . .
(Ⅰ)当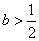 时,判断函数 时,判断函数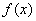 在定义域上的单调性; 在定义域上的单调性;
(Ⅱ)求函数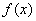 的极值点; 的极值点;
(Ⅲ)证明对任意的正整数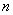 ,不等式 ,不等式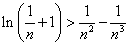 都成立. 都成立.
解(I) 函数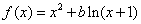 的定义域为 的定义域为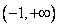 . .
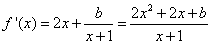 , ,
令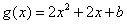 ,则 ,则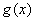 在 在 上递增,在 上递增,在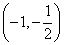 上递减, 上递减,
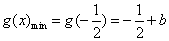 .当 .当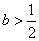 时, 时,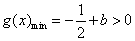 , ,
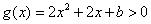 在 在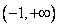 上恒成立. 上恒成立.
即当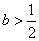 时,函数 时,函数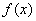 在定义域 在定义域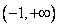 上单调递增。 上单调递增。
(II)分以下几种情形讨论:(1)由(I)知当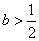 时函数 时函数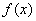 无极值点. 无极值点.
(2)当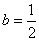 时, 时,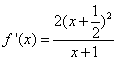 , ,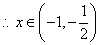 时, 时,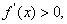
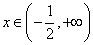 时, 时,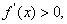 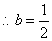 时,函数 时,函数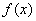 在 在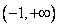 上无极值点。 上无极值点。
(3)当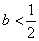 时,解 时,解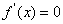 得两个不同解 得两个不同解 , ,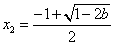 . .
当 时, 时,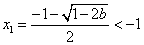 , ,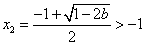 , ,
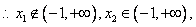
此时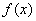 在 在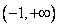 上有唯一的极小值点 上有唯一的极小值点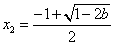 . .
当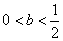 时, 时,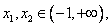
 在 在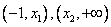 都大于0 , 都大于0 , 在 在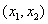 上小于0 , 上小于0 ,
此时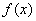 有一个极大值点 有一个极大值点 和一个极小值点 和一个极小值点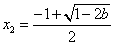 . .
综上可知, 时, 时,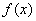 在 在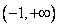 上有唯一的极小值点 上有唯一的极小值点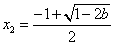 ; ;
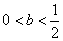 时, 时,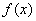 有一个极大值点 有一个极大值点 和一个极小值点 和一个极小值点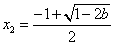 ; ;
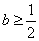 时,函数 时,函数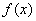 在 在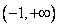 上无极值点。 上无极值点。
(III) 当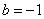 时, 时,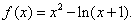
令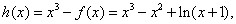 则 则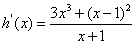 在 在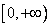 上恒正, 上恒正,
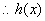 在 在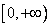 上单调递增,当 上单调递增,当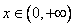 时,恒有 时,恒有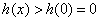 . .
即当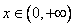 时,有 时,有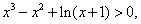 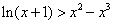 , ,
对任意正整数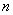 ,取 ,取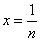 得 得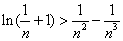
【试题点评】函数的单调性、导数的应用、不等式的证明方法。(I)通过判断导函数的正负来确定函数的单调性是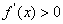 是 是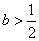 和定义域 和定义域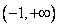 共同作用的结果;(II)需要分类讨论,由(I)可知分类的标准为 共同作用的结果;(II)需要分类讨论,由(I)可知分类的标准为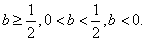 (III)构造新函数为证明不等式“服务”,构造函数的依据是不等式关系中隐含的易于判断的函数关系。用导数解决函数的单调性问题一直是各省市高考及各地市高考模拟试题的重点,究其原因,应该有三条:这里是知识的交汇处,这里是导数的主阵地,这里是思维的制高点.此类问题的一般步骤都能掌握,但重要的是求导后的细节问题------参数的取值范围是否影响了函数的单调性?因而需要进行分类讨论判断:当参数给出了明确的取值范围后,应根据 (III)构造新函数为证明不等式“服务”,构造函数的依据是不等式关系中隐含的易于判断的函数关系。用导数解决函数的单调性问题一直是各省市高考及各地市高考模拟试题的重点,究其原因,应该有三条:这里是知识的交汇处,这里是导数的主阵地,这里是思维的制高点.此类问题的一般步骤都能掌握,但重要的是求导后的细节问题------参数的取值范围是否影响了函数的单调性?因而需要进行分类讨论判断:当参数给出了明确的取值范围后,应根据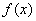 导函数的特点迅速判断 导函数的特点迅速判断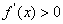 或 或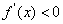 。参数取某些特定值时,可直观作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决.另外要注意由 。参数取某些特定值时,可直观作出判断,单列为一类;不能作出直观判断的,再分为一类,用通法解决.另外要注意由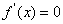 求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为 “极值点”. 求得的根不一定就是极值点,需要判断在该点两侧的异号性后才能称为 “极值点”.
(责任编辑:admin) |
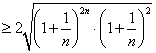
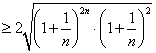
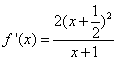 ,
,