|
华东师范大学数学系 陈长华 几何体上的蚂蚁最佳行迹问题，在其展开图是平面图形的立体表面上，蚂蚁从一点爬到另一点时，其最省时的行迹皆为展开图上连接此两点的各直线段中的最短者对应的立主体上的那条曲线段.转化为几何体的侧面展开图上两点间的距离最短问题是解决此类问题的一般的方法.下面我们结合实例来说明侧面展开图的方法. 一、 几何体为棱柱 问题１如图１，长方体ABCD-A1B1C1D1的三条棱长AB=a,AD=b,AA1=c,0<c<b<a,蚂蚁从点A1爬到C，它按怎样的路线爬行，才使其行迹最短. 解：由图１可展开得到展开图１. A1FC与A1HC的线路是相等的. A1HC=  ＝  ，A1EC=  ＝  ,A1GC=  =  ,A1AFC=a＋b＋c. ∵0<c<b<a ∴cb<ca<ab ∴ <<<a＋b＋c即A1HC ＜A1EC＜ A1GC＜A1AFC.由此可见，F、H都是我们所要找的点，易得 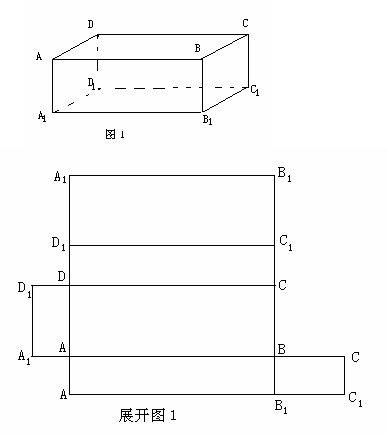 ，利用尺规作图可以找到F和H，从而确定蚂蚁的最佳行迹A1HC或 A1FC. 二、 几何体为棱锥 问题２如图２，课桌上放着一个正三棱锥S-ABC，SA=1,∠ASB=30°, 蚂蚁从点A沿三棱锥的侧面爬行（必须经过三棱锥的三个侧面）再回到A，它按怎样的路线爬行，才使其行迹最短. 解：根据图２，沿SA剪开得展开图２. 在⊿SAE中，  , ,SE= －1.利用尺规作图可以找到E和F，从而确定蚂蚁的最佳行迹AEFA.
三、 几何体为圆锥 问题３如图３，课桌上放着一个圆锥，点A为圆锥底面圆周上一点，SA=3,OA=1蚂蚁从点A沿圆锥的侧面爬行再回到A，它按怎样的路线爬行，才使其行迹最短. 分析：有趣的是蚂蚁的最佳行迹不是底面的圆周，而是向上爬，到达一个最高点后向下爬行. 解：根据图３，沿SA剪开得展开图３. 在⊿SAB中，∠ASB＝  ，AB=3.取SC的中点D，其最佳行迹是曲线段ADB,在侧面展开图上是直线段ADB.  四、 几何体为圆柱 问题４如图４，课桌上放着一个圆柱，蚂蚁从点A沿圆柱的侧面爬行到另一点B，它按怎样的路线爬行，才使其行迹最短. 解：根据图４，沿AE剪开得展开图4. 若点B落在展开图的中位线EF上,则蚂蚁应按AB1或MB１两条线段在圆柱上的对应曲线爬行. 若点B落在展开图的中位线EF的左侧,则蚂蚁应按MB2两条线段在圆柱上的对应曲线爬行. 若点B落在展开图的中位线EF的右侧,则蚂蚁应按AB2两条线段在圆柱上的对应曲线爬行.  五、 几何体为球 问题５如图５，球O的表面上有两点A、B，∠AOB＝  ，蚂蚁从点A沿球的表面爬行到B，它按怎样的路线爬行，才使其行迹最短.解：这时我们知道最佳行迹为AOB所在平面的大圆的劣弧，不能运用初等数学方法来证明这个问题. 我们在此对几何体上的蚂蚁最佳行迹问题进行了讨论，有侧面展开图的通常转化为展开图上的各线段的最短者，来寻求蚂蚁的最佳行迹.没有平面展开图的曲面，寻求最佳行迹就不太方便.这里值得强调的是，立体几何的重要思想方法是将空间问题转化为平面几何问题.  (责任编辑：admin) |
