|
湖南岳阳县七中 胡旭光供稿 一.知识总结 1.函数的奇偶性(首先定义域必须关于原点对称) (1) (2)奇函数 (3)任一个定义域关于原点对称的函数 即 2.函数的单调性(注:①先确定定义域;②单调性证明一定要用定义) (1)定义:区间 (2)奇函数在关于原点对称的区间上单调性相同;偶函数在关于原点对称的区间上单调性相反.判断函数单调性的方法:①定义法,即比差法;②图象法;③单调性的运算性质(实质上是不等式性质);④复合函数单调性判断法则. 3.周期性:周期性主要运用在三角函数及抽象函数中,是化归思想的重要手段.求周期的重要方法:①定义法;②公式法;③图象法;④利用重要结论:若函数f(x)满足f(a-x)=f(a+x),f(b-x)=f(b+x),a≠b,则T=2|a-b|. 二.例题精讲 【例1】已知定义域为 (Ⅰ)求 (Ⅱ)若对任意的 解析:(Ⅰ)因为 即 又由f(1)= -f(-1)知 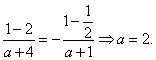 (Ⅱ)由(Ⅰ)知 即 : 整理得 从而判别式 【例2】设函数 解:依题意有 故 从而 令 由于 故 (1) 若 (2) 当 从而 单调减区间为 若 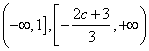 ;单调减区间为 ;单调减区间为【例3】(理)设函数 (文)讨论函数 (理) 解法一:令g(x)=(x+1)ln(x+1)-ax,对函数g(x)求导数:g′(x)=ln(x+1)+1-a 令g′(x)=0,解得x=ea-1-1, (i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,又g(0)=0,所以对x≥0,都有g(x)≥g(0),即当a≤1时,对于所有x≥0,都有 f(x)≥ax. (ii)当a>1时,对于0<x<ea-1-1,g′(x)<0,所以g(x)在(0,ea-1-1)是减函数, 又g(0)=0,所以对0<x<ea-1-1,都有g(x)<g(0),即当a>1时,不是对所有的x≥0,都有f(x)≥ax成立.综上,a的取值范围是(-∞,1]. 解法二:令g(x)=(x+1)ln(x+1)-ax,于是不等式f(x)≥ax成立即为g(x)≥g(0)成立. 对函数g(x)求导数:g′(x)=ln(x+1)+1-a令g′(x)=0,解得x=ea-1-1, 当x>ea-1-1时,g′(x)>0,g(x)为增函数,当-1<x<ea-1-1,g′(x)<0,g(x)为减函数, 所以要对所有x≥0都有g(x)≥g(0)充要条件为ea-1-1≤0.由此得a≤1,即a的取值范围是(-∞,1]. (文)解:设 则 ∵ ∴ 当 当 当 【例4】(理)已知函数 (Ⅰ)若 (Ⅱ)若 (文)已知 (理)   (文)解:∵ 当 ∵ ∴ ∴ 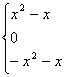 三.巩固练习 1.已知 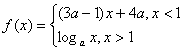 是 是A. 2.已知 A. 3.下列函数中,在其定义域内既是奇函数又是减函数的是( ) A. 4.若不等式 A.0 B. –2 C.- 5.设 A. C. 6.已知定义在 A.-1 B.0 C.1 D.2 7.已知函数 A. 8.(理)如果函数 A. 9.对于 A. 10.已知 A. 11.已知函数 12.已知函数 13. A.5 B.4 C.3 D.2 14.下列函数既是奇函数,又在区间 A. 15.若函数 A.单调递减无最小值 B.单调递减有最小值 C.单调递增无最大值 D.单调递增有最大值 16.若函数 A. 17.设 18.设函数 (Ⅰ)试判断函数 (Ⅱ)试求方程 19. (理)已知 (1)当 (文)已知 (1)求 20.已知函数 (1)求函数 21.已知向量 22. (理)已知函数 (文)已知函数 巩固练习参考答案 1. C 2. D 3. A 4. C 5. D 6. B 7. D 8. B 9. C 10. A 11. a= 18 .解:由f(2-x)=f(2+x),f(7-x)=f(7+x)得函数 从而知函数 由 从而知函数 故函数 (II)由 (II) 又 故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数 在[0,2005]上有402个解,在[-2005.0]上有400个解, 所以函数 19. (理) 解:(I)对函数 令 解得 当
∴ 当 而当 当x=0时, 所以当 (II)当 即 于是 即 (文)解: (1) 先求 设 则点 所以 再根据偶函数的性质, 求当 所以 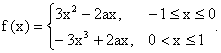 (2) 当 因 因 所以 当 所以 因 所以 (3) 由(2)知 又因 所以 由 20.解:(Ⅰ)由 所以 知 故所求的解析式是 (Ⅱ) 解得 当 当 故 在 21. 解法1:依定义 故要使 解法2:依定义 22. (理) 解: 则 所以 ①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解; ②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解; 则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0. 综上所述,a的取值范围为(-1,0)∪(0,+∞). (文)解: (责任编辑:admin) |
