一、选择题
1. 如果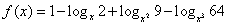 ,则使 ,则使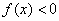 的 的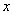 的取值范围为( ) 的取值范围为( )
A. 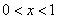 B. B. 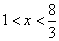 C. C. 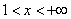 D. D. 
解:显然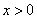 ,且 ,且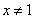 。 。
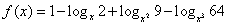 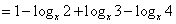 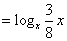 。 。
要使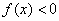 。当 。当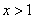 时, 时,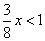 ,即 ,即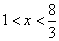 ;当 ;当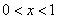 时, 时, ,此时无解。 ,此时无解。
由此可得, 使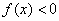 的 的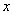 的取值范围为 的取值范围为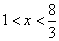 。 应选B。 。 应选B。
2.已知集合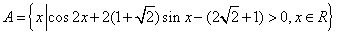 , ,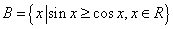 ,则 ,则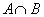 = ( ) = ( )
A.  B. R C. B. R C.  D. D. 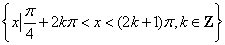
解: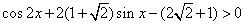
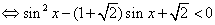 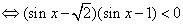
没有实数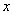 可以使上述不等式成立。故 可以使上述不等式成立。故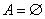 。从而有 。从而有 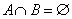 。 应选C。 。 应选C。
3. 以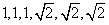 为六条棱长的四面体个数为 ( ) 为六条棱长的四面体个数为 ( )
A. 2 B. 3 C. 4 D. 6
解:以这些边为三角形仅有四种: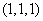 , ,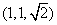 , ,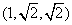 , ,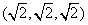 。 。
固定四面体的一面作为底面:
当底面的三边为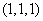 时,另外三边的取法只有一种情况,即 时,另外三边的取法只有一种情况,即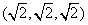 ; ;
当底面的三边为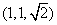 时,另外三边的取法有两种情形,即 时,另外三边的取法有两种情形,即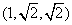 , ,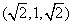 。 。
其余情形得到的四面体均在上述情形中。由此可知,四面体个数有3个。 应选 B。
4. 从1至169的自然数中任意取出3个数构成以整数为公比的递增等比数列的取法有( )种。
A. 89 B. 90 C. 91 D. 92
解:若取出的3个数构成递增等比数列 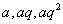 ,则有 ,则有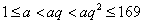 。由此有 。由此有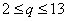 。当 。当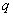 固定时,使三个数 固定时,使三个数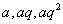 为整数的 为整数的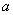 的个数记作 的个数记作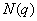 。由 。由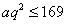 ,知 ,知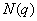 应是 应是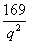 的整数部分。 的整数部分。
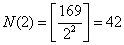 , ,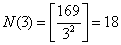 , ,
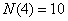 , ,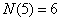 , ,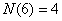 , ,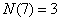 , ,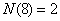 , ,
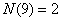 , ,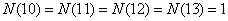 . .
因此,取法共有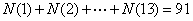 。 应选C 。 应选C
5. 若在复平面上三个点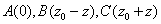 构成以A为直角顶点的等腰直角三角形,其中 构成以A为直角顶点的等腰直角三角形,其中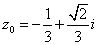 ,则△ABC的面积为( ) ,则△ABC的面积为( )
A. 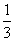 B. B. 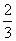 C. 1 D. C. 1 D. 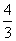
解:依题意, 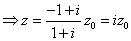 , ,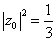 。 。
△ABC的面积为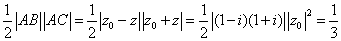 。 应选A。 。 应选A。
6. 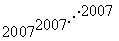 2007重的末二位数字是 ( ) 2007重的末二位数字是 ( )
A. 01 B. 07 C. 43 D. 49
解:记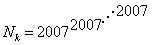 k重。题目要求 k重。题目要求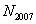 的末二位数。 的末二位数。
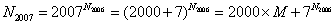
其中M为正整数。由此可得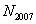 的末二位数与 的末二位数与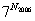 的末二位数字相同。首先来观察 的末二位数字相同。首先来观察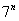 的末二位数字的变化规律。 的末二位数字的变化规律。
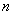
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|

|
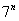 的末二位数字 的末二位数字
|
49
|
43
|
01
|
07
|
49
|
43
|
01
|
07
|

|
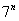 的末二位数字的变化是以4为周期的规律循环出现。 的末二位数字的变化是以4为周期的规律循环出现。
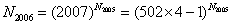 ( (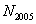 为奇整数) 为奇整数)
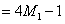 ( (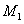 为正整数) 为正整数)
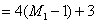
因此,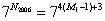 与 与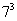 的末二位数字相同,为43。 应选 C。 的末二位数字相同,为43。 应选 C。
二、填空题
7. 设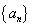 为 为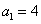 的单调递增数列,且满足 的单调递增数列,且满足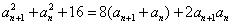 ,则 ,则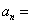 。 。
解: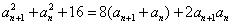
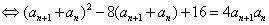
 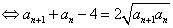 (由题意可知取正号。) (由题意可知取正号。)
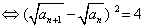 
因此,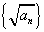 公差为2的等差数列,即 公差为2的等差数列,即 。从而可得 。从而可得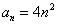 。 答案为 。 答案为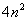 。 。
8. 设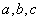 为方程 为方程 的根( 的根(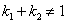 ),则 ),则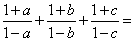 。 。
解: 由题意,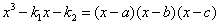 。由此可得 。由此可得
 , ,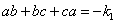 , ,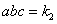 以及 以及 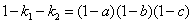 。 。
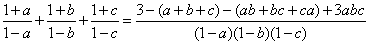 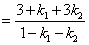 。 。
答案为: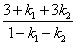 。 。
9. 设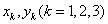 均为非负实数,则 均为非负实数,则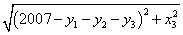 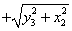 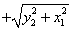
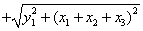 的最小值为 。 的最小值为 。
解: 在直角坐标系中,作点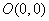 , ,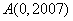 , ,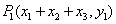 , ,
 , ,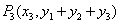 。则 。则
I=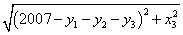 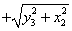 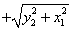 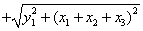
=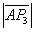 + + + +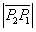 + +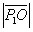 (应用三角不等式) (应用三角不等式)
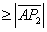 + +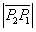 + +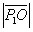 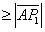 + +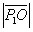 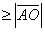 =2007。 =2007。
如果取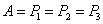 ,即 ,即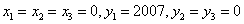 ,那么I取到最小值2007。答案为 2007。 ,那么I取到最小值2007。答案为 2007。
10. 设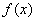 是定义在R上的奇函数,且满足 是定义在R上的奇函数,且满足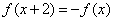 ;又当 ;又当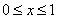 时, 时,
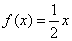 ,则 ,则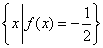 = 。 = 。
解:依题意,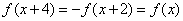 ,即 ,即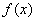 是以4为周期的周期函数。 是以4为周期的周期函数。
因为当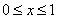 时, 时,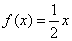 ,且 ,且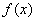 为奇函数,所以当 为奇函数,所以当 时, 时,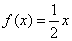 。 。
此时有  。可得 。可得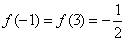 。又因为 。又因为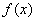 是以4为周期的周期函数, 是以4为周期的周期函数,
所以也有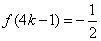 ,( ,(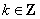 )。 答案为 )。 答案为 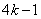 ( (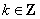 )。 )。
11. 设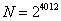 ,则不超过 ,则不超过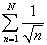 的最大整数为 。 的最大整数为 。
解: 
 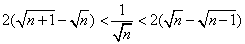 , ,
 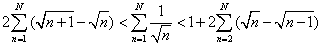 , ,
 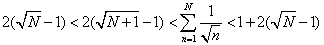 , ,
 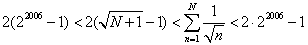 , ,
 不超过 不超过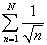 的最大整数为 的最大整数为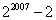 。 答案为 。 答案为 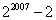 。 。
12. 整数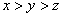 ,且 ,且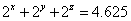 ,则整数组 ,则整数组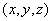 为 。 为 。
解:方程两边同乘以8,得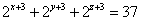 。 因为 。 因为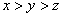 ,所以要使左边为奇数,只有 ,所以要使左边为奇数,只有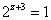 ,即 ,即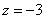 。 。
则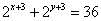 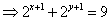 。要使左边为奇数,只有 。要使左边为奇数,只有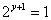 ,即 ,即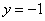 。从而有 。从而有 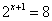 ,即 ,即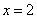 。 。
故有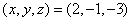 。 答案为 。 答案为  。 。
三、解答题
13. 已知抛物线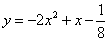 和点 和点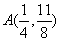 。过点 。过点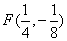 任作直线,交抛物线于B,C两点。 任作直线,交抛物线于B,C两点。
(1) 求△ABC的重心轨迹方程,并表示成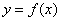 形式; 形式;
(2) 若数列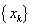 , , ,满足 ,满足 。试证: 。试证: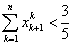 。 。
解:(1)设过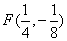 的直线方程为 的直线方程为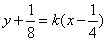 。又设 。又设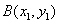 , ,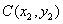 ,联立方程组, ,联立方程组,
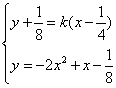
消去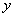 ,得 ,得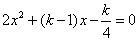 。从而有, 。从而有,
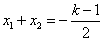 , ,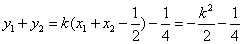 。 ………… 5分 。 ………… 5分
设△ABC的重心坐标为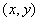 ,则 ,则
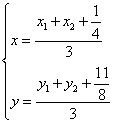 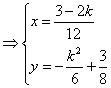
消去k,即得 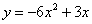 。 …………10分 。 …………10分
(2)因为 , ,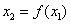 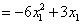 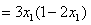 ,所以 ,所以
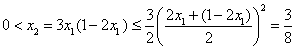 , ,
上式右边等号成立当且仅当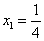 。假设 。假设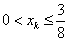 ,则 ,则
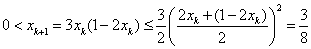 , …………15分 , …………15分
上式右边等号成立当且仅当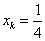 。由此得到 。由此得到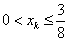 ( (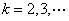 )。从而有 )。从而有
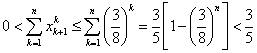 。 …………20分 。 …………20分
14. 设正实数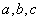 及非负实数 及非负实数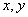 满足条件 满足条件
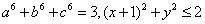
求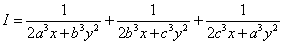 的最小值,并论证之。 的最小值,并论证之。
解:根据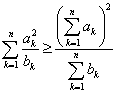 ,有 …………5分 ,有 …………5分
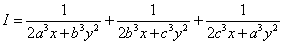
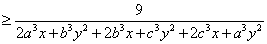 ………… 10分 ………… 10分
 ( (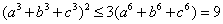 ) )
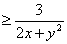 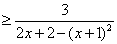 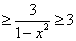 ………… 15分 ………… 15分
上式取等号当且仅当 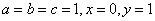 。 ………… 20分 。 ………… 20分
15. 设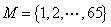 , ,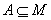 为子集。若 为子集。若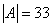 ,且存在 ,且存在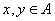 , ,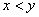 , ,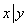 ,则称 ,则称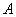 为“好集”。求最大的 为“好集”。求最大的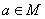 ,使含 ,使含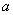 的 任意33元子集为好集。 的 任意33元子集为好集。
解:令 , ,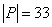 。 。
显然对任意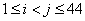 ,不存在 ,不存在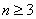 ,使得 ,使得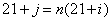 成立。故P是非好集。 成立。故P是非好集。
因此 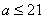 。 …………5分 。 …………5分
下面证明:包含21的任意一个33元子集A一定为好集。
设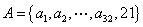 。 。
若1,3,7,42,63中之一为集合A的元素,显然为好集。 …………10分
现考虑1,3,7,42,63都不属于集合A。构造集合
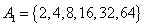 , ,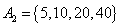 , ,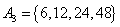 , ,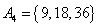 , ,
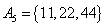 , ,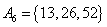 , ,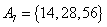 , ,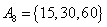 , ,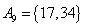
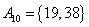 , ,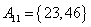 , ,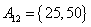 , ,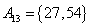 , ,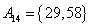 , ,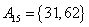 , ,
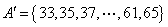 。 ………… 15分 。 ………… 15分
由上可见,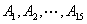 每个集合中两个元素都是倍数关系。考虑最不利的情况,即 每个集合中两个元素都是倍数关系。考虑最不利的情况,即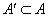 ,也即 ,也即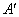 中16个元素全部选作A的元素,A中剩下16个元素必须从 中16个元素全部选作A的元素,A中剩下16个元素必须从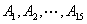 这15个集合中选取16个元素。根据抽屉原理,至少有一个集合有两个元素被选,即集合A中至少有两个元素存在倍数关系。 这15个集合中选取16个元素。根据抽屉原理,至少有一个集合有两个元素被选,即集合A中至少有两个元素存在倍数关系。
综上所述,包含21的任意一个33元子集A一定为好集,即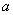 的最大值为21。 ……20分 的最大值为21。 ……20分
(责任编辑:admin) |
 。可得
。可得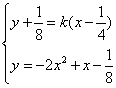
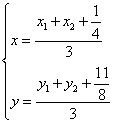
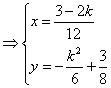
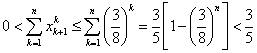 。 …………20分
。 …………20分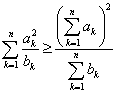 ,有 …………5分
,有 …………5分