|
北大附中高一(1 周栋 谭思睿 所谓理论保级分数，就是指一般来讲，一个参赛球队只要达到了这个分数，无论别的球队的成绩如何，都能保证自己不会降级。这个分数无疑能给那些成绩不佳的球队的一个有效的参考，帮助他们调整策略。 当然，不仅是我国的足球联赛，其它各个国家的足球联赛，都会有保级分数的问题。 那么这个理论保级分数应该如何计算呢？怎样找到一种普遍适用于各国足球联赛的计算理论保级分数的方法呢？下面，我们建立一个数学模型解决这个问题。 模型建立与分析 要想研究理论保级分数，就必须研究每支球队在每场比赛中的成绩。通过观察各大联赛的比赛情况，我们可以知道，球队的实力对比赛结果有很大的影响。比如，实力差距比较大的两支球队比赛，实力强的一方获胜的希望比较大。所以，如果讨论联赛的积分情况，就不能回避球队实力的差异问题。 但是球队的实力是一个很抽象的事物，不易计算和比较，为了能用数学语言描述它，可以为每个球队引入一个参数，能够较好的描述球队的实力称它为这个球队的实力数，我们可以定义随机变量X为一支球队在某一场比赛中的结果。它可能有三种情况，即胜（积3分）、平（积1分）、负（积0分〕。我们可以统计出每场比赛中两队的胜、平、负的频率（可近似地看成每种情况出现的概率）P，通过公式 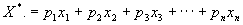 求出一支球队在每场比赛中的数学期望 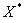 。将所有比赛的数学期望值相加，就可以求出理论上这支球队的最后积分。另外，应该注意到主客场的差异对比赛结果的影响。所以，如果主客场情况不同，相应的胜、负、平频率也不同，数学期望值也就不同。 一、模型假设 1．假设参加某一联赛的所有球队的实力数由小（实力强）到大（实大弱）可构成一个等差数列。并且认为等差数列的首项为1，公差为1。由此，一个联赛中的各个球队可以分别用一个数字代替，即，将所有n支参赛球队按实力由强到弱排列,则依次1,2,3,4，...,n。这样每场比赛就有一个对应的实力数之差。如实力数为3和7的两支球队之间的比赛，实力差是4。 2．假设任何不可预知的因素与比赛结果无关。即比赛结果只与两支球队的实力差和主客场因素有关。如认为球队3主场与球队8的比赛，和球队1主场与球队6的比赛没有任何区别。 3．假设统得出的每个实力差值对应的比胜、负、平的频率等于在理论上这些情况出现的频率。 二、定义变量 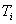 ：一支球队在一场比赛中的数学期望值。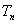 ：一支球队i在所有比赛中的数学期望值之和。n:参加联赛的球队总数。 m：联赛结束后将要降级的球队数目。 s：一场比赛中实力较强的球队获胜的概率。 p：一场比赛中实力较强的球队战平的概率。 f：一场比赛中实力较强的球队失败的概率。 解决问题 一、统计随机变量X的分布 我们选取了英格兰足球超级联赛、德国足球甲级联赛、意大利足球甲级联赛、中国的甲级联赛中1999～2000赛季的详细情况，并根据这些数据统计了当实力数差分别为1,2,3,...，19时，较强的一方获胜、战平、战败的频率。如下表：（单位：％）
二、计算各队的理论积分 有了这些数据之后，我们可以根据求随机变量的数学期望的公式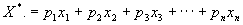： 求出一支球队在同比自己实力弱的球队的比赛里的教学期望。即 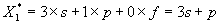 当一支球队和比自己实力强的球队比赛时，实力较强球队的战败概率就是实力较弱的球队的获胜概率。即 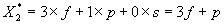 这样一来，所有比赛的数学期望都能求出。也就是说，对于每一支球队，其所有比赛数学期望值的和也能求出，我们用 根据这种思路，我们使用VisualBasic6.0编制一个程序来计算理论保级分数。 算法简要说明 1.输入数据：将计算所需的变量n、m通过文本框Textl、Text2输入程序中。 2.定义数组：将统计得出的s、p、f各概率值定义为三个数组s()、p()、以便赋值。再定义数列{ 3．对概率赋值：将统计得的概率数据赋至各个数组中。 4．通过循环嵌套，计算最后每支球队的理论积分，即各个数学期望之和。 5．将恰好保级的一支球队的分数输出之文本框Text3中。 具体源代码及说明（略） 运行源程序，得出下表数据：
这样，一般的足球联赛都能通过这个程序求出理论保级分数。 验证模型 以上，给出了足球联赛中的理论保级分数的一种计算方法，这种方法是否理想？得出的结论能否令人满意？下面，我们通过计算值与实际值的对比，来验证这个模型。 首先，我们看2000年的甲A联赛。下表是该赛季最终的排名情况。
去掉两个降级球队的分数，保级分数是29分。经过上述算法，将n=14，m=2代入，计算得来的理论保级分数是28.5259分，可见，与实际保级分数相差不大。 再看看上赛季意大利足球甲级联赛,去掉3个降级的球队,实际保级分数是36分。将n=18,m=3代入，计算的理论保级分数是34.5975分，与实际情况也相差不大。 虽然用这个程序计算的保级分数有时会与实际分数有一点差距，但在大多数情况下，这个程序能够较好地估计保级分数。 误差分析 这个模型中可能产生误差的地方有如下几处： 一、在模型假设中，假设各球队的实力数构成等差数列。这种假设与实际情况有一定差距。 二、在统计概率过程中，随着n值不断增大，能找到的比赛数量越来越少。所以在n较大时，统计出的频率与理论上的频率的偏差也就比较大。 三、在实际比赛中，很多其它因索，如天气等都有可能影响比赛的结果。这个模型并没有考虑这些因素，所以无法避免由此产生的误差。 由于以上几种可能产生误差的原因，这个模型计算的结果与实际保级分数有大约6分以下的差距。由于一般情况下这个模型计算的结果比较合适，所以认为这样的误差在可以接受的范围内。 参考资料 1．《问题解决的数学模型》，刘来福、曾文艺著，北京师范大学出版社。 2.《中学数学知识应用精编》，上海市中学生数学知识应用大竞赛委员会编写组著，华东理工大学出版社。 3．《数学建模精品案例》，朱道元编著，东南大学出版社。 （选自《中学生数学》期刊2001年11月上） |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||