36、(全国卷二理)已知函数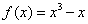 . .
(1)求曲线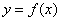 在点 在点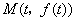 处的切线方程; 处的切线方程;
(2)设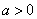 ,如果过点 ,如果过点 可作曲线 可作曲线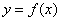 的三条切线,证明: 的三条切线,证明:
解:(1) 的导数 的导数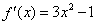 .曲线 .曲线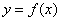 在点 在点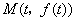 处的切线方程为: 处的切线方程为: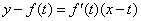 ,即 ,即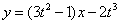 . .
(2)如果有一条切线过点 ,则存在 ,则存在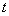 ,使 ,使 . .
若过点 可作曲线 可作曲线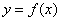 的三条切线,则方程 的三条切线,则方程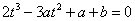 有三个相异的实数根.记 有三个相异的实数根.记 ,则 ,则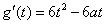 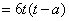 . .
当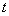 变化时, 变化时,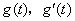 变化情况如下表: 变化情况如下表:
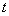
|

|
0
|
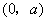
|
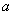
|
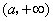
|
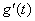
|

|
0
|
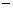
|
0
|

|
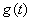
|
增函数
|
极大值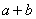
|
减函数
|
极小值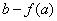
|
增函数
|
由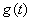 的单调性,当极大值 的单调性,当极大值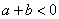 或极小值 或极小值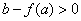 时,方程 时,方程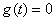 最多有一个实数根; 最多有一个实数根;
当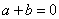 时,解方程 时,解方程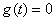 得 得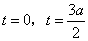 ,即方程 ,即方程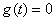 只有两个相异的实数根; 只有两个相异的实数根;
当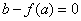 时,解方程 时,解方程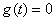 得 得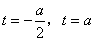 ,即方程 ,即方程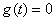 只有两个相异的实数根. 只有两个相异的实数根.
综上,如果过 可作曲线 可作曲线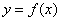 三条切线,即 三条切线,即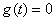 有三个相异的实数根,则 有三个相异的实数根,则 即 即  . .
37、(全国卷一理)设函数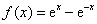 . .
(Ⅰ)证明: 的导数 的导数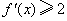 ; ;
(Ⅱ)若对所有 都有 都有 ,求 ,求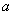 的取值范围. 的取值范围.
解:(Ⅰ) 的导数 的导数 .由于 .由于 ,故 ,故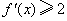 . .
(当且仅当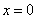 时,等号成立). 时,等号成立).
(Ⅱ)令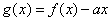 ,则 ,则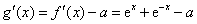 , ,
(ⅰ)若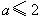 ,当 ,当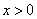 时, 时, , ,
故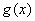 在 在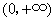 上为增函数, 上为增函数,
所以, 时, 时,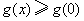 ,即 ,即 . .
(ⅱ)若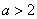 ,方程 ,方程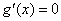 的正根为 的正根为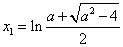 , ,
此时,若 ,则 ,则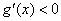 ,故 ,故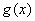 在该区间为减函数. 在该区间为减函数.
所以, 时, 时, ,即 ,即 ,与题设 ,与题设 相矛盾. 相矛盾.
综上,满足条件的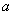 的取值范围是 的取值范围是 . .
38、(江西理)如图,函数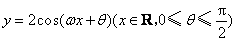 的图象与 的图象与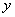 轴交于点 轴交于点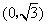 ,且在该点处切线的斜率为 ,且在该点处切线的斜率为 . .
(1)求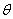 和 和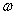 的值; 的值;
(2)已知点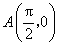 ,点 ,点 是该函数图象上一点,点 是该函数图象上一点,点 是 是 的中点,当 的中点,当 , ,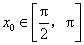 时,求 时,求 的值. 的值.
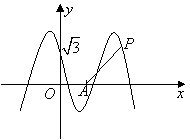
解:(1)将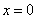 , , 代入函数 代入函数 得 得 ,因为 ,因为 ,所以 ,所以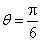 . .
又因为 , ,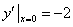 , ,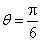 ,所以 ,所以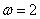 ,因此 ,因此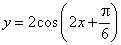 . .
(2)因为点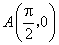 , , 是 是 的中点, 的中点, ,点 ,点 的坐标为 的坐标为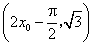 . .
又因为点 在 在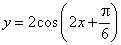 的图象上,所以 的图象上,所以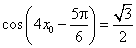 . .
因为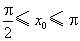 ,所以 ,所以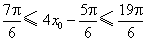 , ,
从而得 或 或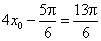 .即 .即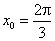 或 或 . .
39、(湖南理)如图,某地为了开发旅游资源,欲修建一条连接风景点 和居民区 和居民区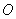 的公路,点 的公路,点 所在的山坡面与山脚所在水平面 所在的山坡面与山脚所在水平面 所成的二面角为 所成的二面角为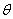 ( (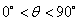 ),且 ),且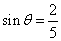 ,点 ,点 到平面 到平面 的距离 的距离 (km).沿山脚原有一段笔直的公路 (km).沿山脚原有一段笔直的公路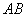 可供利用.从点 可供利用.从点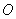 到山脚修路的造价为 到山脚修路的造价为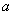 万元/km,原有公路改建费用为 万元/km,原有公路改建费用为 万元/km.当山坡上公路长度为 万元/km.当山坡上公路长度为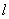 km( km(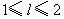 )时,其造价为 )时,其造价为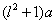 万元.已知 万元.已知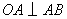 , ,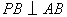 , ,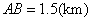 , ,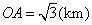 . .
(I)在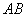 上求一点 上求一点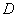 ,使沿折线 ,使沿折线 修建公路的总造价最小; 修建公路的总造价最小;
(II)对于(I)中得到的点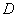 ,在 ,在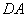 上求一点 上求一点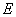 ,使沿折线 ,使沿折线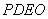 修建公路的总造价最小. 修建公路的总造价最小.
(III)在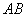 上是否存在两个不同的点 上是否存在两个不同的点 , , ,使沿折线 ,使沿折线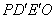 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论. 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
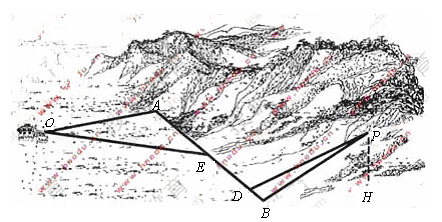
解:(I)如图, , , , ,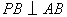 , ,
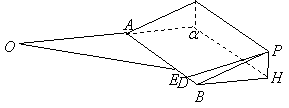
由三垂线定理逆定理知, ,所以 ,所以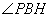 是山坡与 是山坡与 所成二面角的平面角,则 所成二面角的平面角,则 , ,
 .设 .设 , ,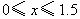 . .
则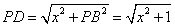 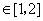 . .
记总造价为 万元, 万元,
据题设有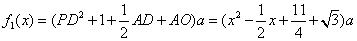

当 ,即 ,即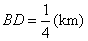 时,总造价 时,总造价 最小. 最小.
(II)设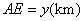 , , ,总造价为 ,总造价为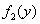 万元,根据题设有 万元,根据题设有
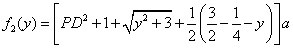  . .
则 ,由 ,由 ,得 ,得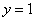 . .
当 时, 时,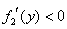 , ,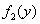 在 在 内是减函数; 内是减函数;
当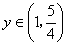 时, 时,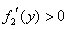 , ,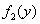 在 在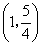 内是增函数. 内是增函数.
故当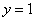 ,即 ,即 (km)时总造价 (km)时总造价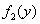 最小,且最小总造价为 最小,且最小总造价为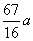 万元. 万元.
(III)解法一:不存在这样的点 , , . .
事实上,在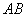 上任取不同的两点 上任取不同的两点 , , .为使总造价最小, .为使总造价最小,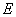 显然不能位于 显然不能位于 与 与 之间.故可设 之间.故可设 位于 位于 与 与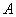 之间,且 之间,且 = =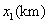 , , , , ,总造价为 ,总造价为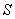 万元,则 万元,则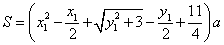 .类似于(I)、(II)讨论知, .类似于(I)、(II)讨论知,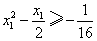 , , ,当且仅当 ,当且仅当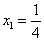 , , 同时成立时,上述两个不等式等号同时成立,此时 同时成立时,上述两个不等式等号同时成立,此时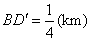 , , , ,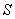 取得最小值 取得最小值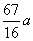 ,点 ,点 分别与点 分别与点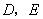 重合,所以不存在这样的点 重合,所以不存在这样的点  ,使沿折线 ,使沿折线 修建公路的总造价小于(II)中得到的最小总造价. 修建公路的总造价小于(II)中得到的最小总造价.
解法二:同解法一得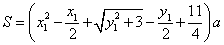
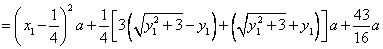
 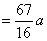 . .
当且仅当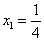 且 且 ,即 ,即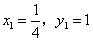 同时成立时, 同时成立时,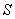 取得最小值 取得最小值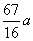 ,以上同解法一. ,以上同解法一.
40、(湖北理)已知定义在正实数集上的函数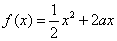 , ,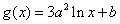 ,其中 ,其中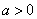 .设两曲线 .设两曲线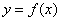 , , 有公共点,且在该点处的切线相同. 有公共点,且在该点处的切线相同.
(I)用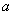 表示 表示 ,并求 ,并求 的最大值; 的最大值;
(II)求证: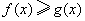 ( (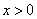 ). ).
本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
解:(Ⅰ)设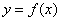 与 与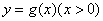 在公共点 在公共点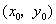 处的切线相同. 处的切线相同.
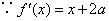 , , ,由题意 ,由题意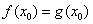 , , . .
即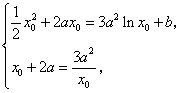 由 由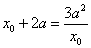 得: 得: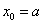 ,或 ,或 (舍去). (舍去).
即有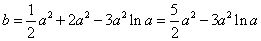 . .
令 ,则 ,则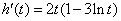 .于是 .于是
当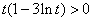 ,即 ,即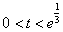 时, 时,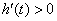 ; ;
当 ,即 ,即 时, 时, . .
故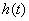 在 在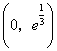 为增函数,在 为增函数,在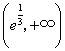 为减函数, 为减函数,
于是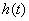 在 在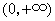 的最大值为 的最大值为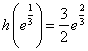 . .
(Ⅱ)设 , ,
则  . .
故 在 在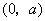 为减函数,在 为减函数,在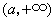 为增函数, 为增函数,
于是函数 在 在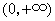 上的最小值是 上的最小值是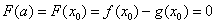 . .
故当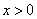 时,有 时,有 ,即当 ,即当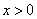 时, 时, . .
(责任编辑:admin)
|



 ,由
,由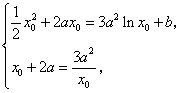 由
由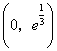 为增函数,在
为增函数,在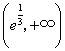 为减函数,
为减函数,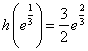 .
.