谈椭圆扁平的判定
广东省中山一中高中部 许少华
我们知道,椭圆的离心率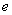 满足 满足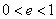 ,当 ,当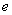 越接近于1时, 越接近于1时,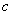 就越接近于 就越接近于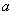 ,从而 ,从而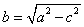 就越小,此时,椭圆就越扁;当 就越小,此时,椭圆就越扁;当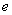 越接近于0时, 越接近于0时,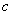 就越接近 就越接近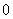 ,从而 ,从而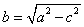 就越近于 就越近于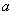 ,此时,椭圆就越接近于圆;下面 我们来探究三个问题: ,此时,椭圆就越接近于圆;下面 我们来探究三个问题:
探究一:能否借助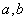 与 与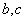 来刻画椭圆的扁平程度? 来刻画椭圆的扁平程度?
首先,我们来看能否用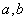 来刻画椭圆的扁平程度,由于 来刻画椭圆的扁平程度,由于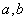 越接近,椭圆就越“圆”, 越接近,椭圆就越“圆”,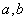 相差越大,椭圆就越“扁”,因此,可以用 相差越大,椭圆就越“扁”,因此,可以用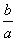 来刻画椭圆的扁平程度。当 来刻画椭圆的扁平程度。当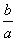 越接近于1时,椭圆就越“圆”,当 越接近于1时,椭圆就越“圆”,当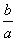 越小时,椭圆就越“扁”。 越小时,椭圆就越“扁”。
再看能否用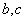 来刻画椭圆的扁平程度,结合 来刻画椭圆的扁平程度,结合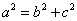 可以看出: 可以看出: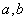 越接近, 越接近,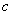 就越接近 就越接近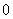 , ,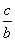 也越接近 也越接近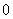 ,此时,椭圆就越“圆”; ,此时,椭圆就越“圆”;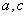 越接近, 越接近,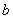 就越接近 就越接近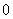 , ,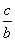 无限大,此时,椭圆就越“扁”。 无限大,此时,椭圆就越“扁”。
显然,既可以用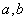 来刻画椭圆的扁平程度,也可以用 来刻画椭圆的扁平程度,也可以用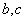 来刻画椭圆的扁平程度。 来刻画椭圆的扁平程度。
探究二:为什么选用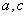 来刻画椭圆的扁平程度? 来刻画椭圆的扁平程度?
第一,椭圆的“圆”的程度用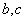 容易刻画,即 容易刻画,即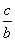 越接近 越接近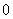 时,椭圆就越“圆”;但在表示“扁”时,用 时,椭圆就越“圆”;但在表示“扁”时,用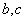 很不明确,“ 很不明确,“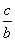 无限大,此时,椭圆就越“扁””,大的程度无法把握。 无限大,此时,椭圆就越“扁””,大的程度无法把握。
第二,对于椭圆,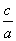 的范围是 的范围是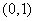 , ,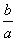 的范围也是 的范围也是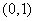 ;且两者都可以较好的刻画椭圆的扁平程度,表面上看它们具有等同的位置。将这两个量再放入圆锥曲线之中,就可以发现选用 ;且两者都可以较好的刻画椭圆的扁平程度,表面上看它们具有等同的位置。将这两个量再放入圆锥曲线之中,就可以发现选用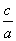 是应该的。因为,在以后将要学习的双曲线、抛物线中,正好填补了 是应该的。因为,在以后将要学习的双曲线、抛物线中,正好填补了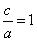 与 与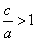 的两种情况。考虑到整体内容,选用了 的两种情况。考虑到整体内容,选用了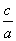 。 。
探究三: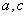 将会有哪些变化? 将会有哪些变化?
例1、设椭圆的两个焦点分别为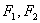 ,过 ,过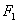 作椭圆长轴的垂线交椭圆于点 作椭圆长轴的垂线交椭圆于点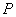 ,若 ,若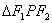 为等腰直角三角形,则椭圆的离心率为( ) 为等腰直角三角形,则椭圆的离心率为( )
(A)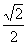 (B) (B)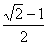 (C) (C)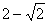 (D) (D)
解析:设椭圆方程为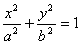 ,由 ,由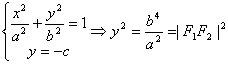 即 即
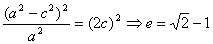 ,选D; ,选D;
评析:本题重在产生关于 的关系式,将关系式转化为关于离心率 的关系式,将关系式转化为关于离心率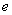 的方程通过方程产生结论。 的方程通过方程产生结论。
例2、椭圆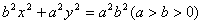 和圆 和圆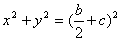 有四个交点,其中 有四个交点,其中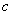 为椭圆的半焦距,则椭圆离心率 为椭圆的半焦距,则椭圆离心率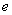 的范围为( ) 的范围为( )
(A)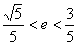 (B) (B)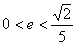 (C) (C)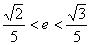 (D) (D)
解析:此题的本质是椭圆的两个顶点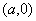 与 与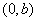 一个在圆外、一个在圆内即: 一个在圆外、一个在圆内即:

评析:建立在条件的基础上,产生关于 的不等关系式,再将其转化为关于离心率 的不等关系式,再将其转化为关于离心率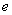 的不等式是关键。 的不等式是关键。
例3、已知c是椭圆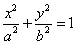 (a>b>0)的半焦距,则 (a>b>0)的半焦距,则 的取值范围是 ( ) 的取值范围是 ( )
(A)(1,+∞) (B)(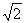 ,+∞) (C)(1, ,+∞) (C)(1,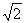 ) (D)(1, ) (D)(1,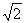 ] ]
解析:由 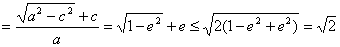 ,又 ,又
于是得答案(D);
评析:如何求 的取值范围,结合离心率及关系式 的取值范围,结合离心率及关系式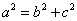 ,将待求式子转化为关于 ,将待求式子转化为关于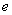 的函数关系,借助函数的定义域(即 的函数关系,借助函数的定义域(即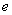 的范围)产生函数的值域。 的范围)产生函数的值域。
例4、已知椭圆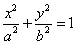 ( (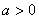 , ,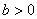 )左、右焦点为 )左、右焦点为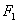 、 、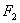 ,左准线 ,左准线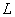 , ,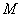 是椭圆上的一点,并且有 是椭圆上的一点,并且有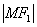 是点 是点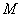 到 到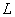 的距离 的距离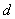 与 与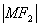 的等比中项,求该椭圆离心率 的等比中项,求该椭圆离心率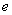 的最大值. 的最大值.
解析一 设点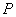 的坐标为 的坐标为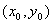 ,其中 ,其中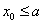 .由椭圆的第二定义可知: .由椭圆的第二定义可知: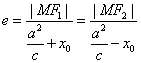 ,又由已知可得: ,又由已知可得: 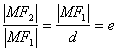 ,则有: ,则有: .代入得: .代入得:  
考虑椭圆离心率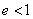 ,解得: ,解得: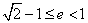 .因此,该椭圆离心率e的最小值为 .因此,该椭圆离心率e的最小值为 ; ;
解析二 由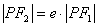 ,又由得 ,又由得 ,因此 ,因此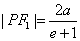 , ,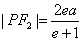 ,又由 ,又由 ,则: ,则: 
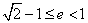 因此,该椭圆离心率e的最小值为 因此,该椭圆离心率e的最小值为 ; ;
评析:离心率的最值也是我们经常遇到的问题,在最值的求解过程中,抓问题的转折点很关键,解一中“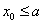 ”、解二中“ ”、解二中“ ”都是关键点,没有这两点两种方法都无法产生结论。 ”都是关键点,没有这两点两种方法都无法产生结论。
好了,经过这一番的探究,你有收获吗?
(责任编辑:admin)
|
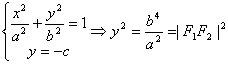 即
即
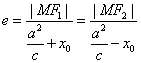 ,又由已知可得:
,又由已知可得: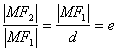 ,则有:
,则有: