探寻解三角形的入手策略
http://www.newdu.com 2025/05/19 11:05:51 人民教育出版社 佚名 参加讨论
探寻解三角形的入手策略 内蒙古赤峰市翁牛特旗乌丹一中 熊明军 解三角形知识一直是高考常考考点，虽然这一块儿只要运用公式、正弦定理与余弦定理便能解决很多问题，但是如何针对试题，灵活、准确、快速地选定相关定理去入手解题，则是同学们很难把握的。本文结合具体题目，初步探寻一些入手策略，期望对同学们有所帮助。 【正弦定理公式】  ；【余弦定理公式】  ； ； 如果将公式、正弦定理、余弦定理看成是几个“方程”的话，那么解三角形的实质就是把题目中所给的已知条件按方程的思想进行处理，解题时根据已知量与所求量，合理选择一个比较容易解的方程（公式、正弦定理、余弦定理），从而使同学们入手容易，解题简洁。 一、直接运用公式、正弦定理、余弦定理 （1）三角公式 ①在  中，已知两角 的三角函数值，求第三个角 ；存在  。证明： 有解 有解  即，要判断是否有解，只需 。（2）正弦定理 ①在 中，已知两角和任意一边，解三角形；②在 中，已知两边和其中一边对角，解三角形；（3）余弦定理 ①在 中，已知三边，解三角形；②在 中，已知两边和他们的夹角，解三角形。直接运用正弦定理、余弦定理的上述情况，是我们常见、常讲、常练的，因此，在这里就不加赘述，同学们可以自己从教材中找一些题目看一看！ 二、间接运用公式、正弦定理、余弦定理 （1）齐次式条件（边或角的正弦） 若题目条件中出现关于角的齐次式或关于边的齐次式，可以根据角的异同选用公式弦切互化或正弦定理边角互化；有些题中没有明显的齐次式，但经过变形得到齐次式的依然适用。 1.相同角齐次式条件的弦切互化 【例】在 中，若 ， ，求。【解析】无论是条件中的 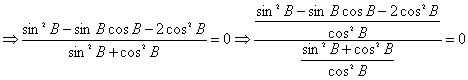 ，还是 都是关于一个角的齐次式。 是关于 的一次齐次式； 是关于 的二次齐次式。因此，我们将弦化切，再利用三角公式求解。由  ；由    或 ；在 中， ，且 。代值可得：①当  ，时， ；②当 ， 时， （舍去）。2.不同角（正弦）齐次式条件的边角互化 【例】在 中，若 ，且 ，求的面积。【解析】条件是关于不同角正弦的二次齐次式。因此，我们利用正弦定理将角化为边，然后根据边的关系利用余弦定理求解。由  ；显然这个形式符合余弦定理的公式，因此，可得  。又因为  ，所以 。3.不同边齐次式条件的边角互化 【例】 的内角 的对边分别为 。已知 ， ，求。【解析】条件 是关于不同边的一次齐次式。因此，我们利用正弦定理将边化为角，然后由 将不同角转化为同角,利用化一公式求解。由  ，又 ， ，可得： ，运用化一公式得 。4.边角混合齐次式条件的边角互化 ①边角混合——边为齐次式 【例】 的内角的对边分别为，且 ，求 。【解析】条件 是边角混合——关于不同边的一次齐次式，由于所求为切的值，所以将边化为角，然后将弦化为切求解。由  ，又 ，则  。②边角混合——角（正弦）为齐次式 【例】 的内角 的对边分别为 ，且 ， ，求。【解析】条件  是边角混合——角（正弦）为不同角的一次齐次式。因此，我们将角的正弦化为边，然后根据等式形式利用余弦定理求解。由  ，由于，我们可以得到： ，显然这个形式符合余弦定理公式，因此，可得 。从而得出 。③边角混合——边、角（正弦）都为齐次式 【例】 的内角的对边分别为，且 ，求。【解析】条件 是边角混合——边、角（正弦）各为一次齐次式。因此，我们可以随意边角互化，但是一般将角转化为边求解。由  ，显然这个形式符合余弦定理公式，因此，可得  。从而得出  。5.非三角形内角正弦但可化为角（正弦）齐次式 【例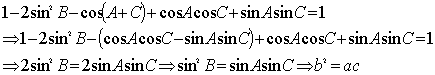】 的内角的对边分别为，且 ，求证：的三边成等比数列。【解析】条件 显然不是齐次式，并且角也不全是三角形的内角。因此，首先得把这些角转变为三角形的内角，然后再往齐次式化利用正弦定理求解。由  ，只要将 变换为 ，题中的条件就变成了关于不同内角正弦的二次齐次式： 。（2）不同边的平方关系（余弦定理） 若题目条件中出现关于边的平方关系或求边的平方关系，可以选用余弦定理边角互化，在上面的一些情况中，有利用正弦定理转化出不同边的平方关系，可以作为参考例题。 【例】 的内角的对边分别为，且 ，求。【解析】条件 含有不同边的平方关系，形式显然符合余弦定理公式。由  。（3）存在消不掉的正弦、余弦值（两定理同时使用，边角互化） 若题目条件中的条件不是上述情况，且始终含有消不去的内角正弦、余弦，可以同时使用正弦、余弦定理边角互化，要么都化为角（正弦、余弦），要么都化为边。 【例】在 中，已知 ，且 ，求 。【解析】由题目中条件  可得 ，接下来再利用余弦定理可得  ，又 ， ，所以 或 。因为  。解三角形运用的原理简单，但是题目灵活多变，往往使学生感觉不易下手，以上结合例题谈了一下通过题中条件的特征，利用三角形内角和、边、角之间的关系快速入手的策略，但这仅仅是初探，更多的策略还需要同学们在解题中不断地归纳总结。 (责任编辑：admin) |