构建仿射坐标系解题
湖北省阳新县高级中学 邹生书
直角坐标系和斜角坐标系统称为仿射坐标系,直角坐标系是仿射坐标系的特例,斜角坐标系是直角坐标系的类比推广.本文通过类比直角坐标系下点的坐标、向量坐标、直线方程等有关知识,构建仿射坐标系解决向量共线、向量线性表示以及线性规划等有关问题.
一、仿射坐标系下的向量共线问题
我们知道在直角坐标系下共线向量有如下结论:若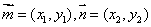 ,则 ,则 。同样在仿射坐标系下此结论仍然成立。 。同样在仿射坐标系下此结论仍然成立。
例1 已知向量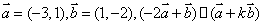 ,则实数 ,则实数 的值是( ) 的值是( )
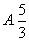  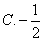 
解法1(常规解法)因 ,故 ,故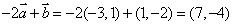 , ,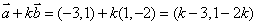 .又 .又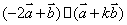 ,所以 ,所以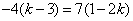 ,解得 ,解得 ,故选 ,故选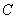 . .
解法2 由 ,知 ,知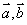 不共线,以原直角坐标系的原点 不共线,以原直角坐标系的原点 作为原点,以 作为原点,以 作为单位基底建立仿射坐标系 作为单位基底建立仿射坐标系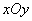 , 则 , 则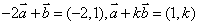 ,因为 ,因为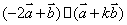 ,所以 ,所以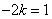 ,所以 ,所以 ,故选 ,故选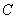 . .
例2 已知向量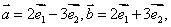 其中 其中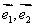 不共线,向量 不共线,向量 .问是否存在这样的非零实数 .问是否存在这样的非零实数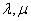 ,使向量 ,使向量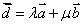 与 与 共线? 共线?
解法1(常规解法) 因为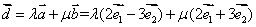 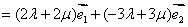 ,若 ,若 与 与 共线,因 共线,因 ,所以存在实数 ,所以存在实数 ,使得 ,使得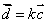 ,即 ,即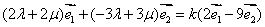 ,所以 ,所以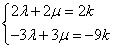 ,消去 ,消去 得 得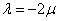 ,故存在这样的非零实数 ,故存在这样的非零实数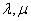 ,只要 ,只要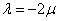 ,就能使向量 ,就能使向量 与 与 共线. 共线.
解法2 因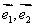 不共线,在向量平面内任取一点 不共线,在向量平面内任取一点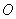 作为原点,以 作为原点,以 作为单位基底建立仿射坐标系 作为单位基底建立仿射坐标系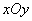 ,则 ,则 ,同法1得 ,同法1得 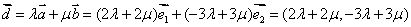 . .
若向量 与 与 共线,则 共线,则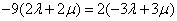 ,解得 ,解得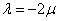 ,故存在这样的非零实数 ,故存在这样的非零实数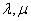 ,只要 ,只要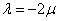 ,就能使向量 ,就能使向量 与 与 共线. 共线.
二、仿射坐标系下向量的线性表示问题
例3 如图1,在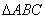 中, 中,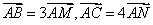 , , 和 和 交于点 交于点 .试用向量 .试用向量 和 和 表示向量 表示向量 . .
解 以 为坐标原点,以 为坐标原点,以 作为仿射坐标系的单位基底, 作为仿射坐标系的单位基底,
建立平面仿射坐标系如图1所示.因为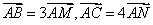 ,所以 ,所以
 , , .所以直 .所以直
线 在仿射坐标系下的“截距式”方程为 在仿射坐标系下的“截距式”方程为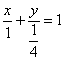 即 即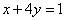 ①. ①.
直线 在仿射坐标系下的“截距式”方程为 在仿射坐标系下的“截距式”方程为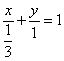 即 即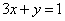 ②.解①②得 ②.解①②得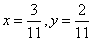 ,则点 ,则点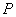 的坐标为 的坐标为 ,所以 ,所以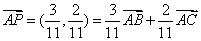 . .

图1
例4 在平行四边形 中, 中,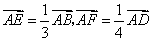 , ,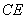 与 与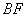 相交于 相交于 点,若 点,若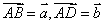 ,则 ,则 ( ) ( )
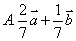 
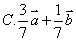 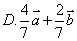
解 以 为坐标原点,以 为坐标原点,以 作为仿射坐标系的单位基底,建立平面仿射坐标系如图2所示.因为 作为仿射坐标系的单位基底,建立平面仿射坐标系如图2所示.因为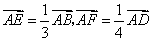 ,所以 ,所以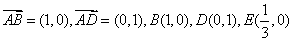 , , 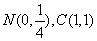 .所以直线 .所以直线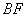 在仿射坐标系下的“截距式”方程为 在仿射坐标系下的“截距式”方程为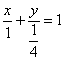 即 即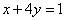 ①.直线 ①.直线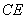 在仿射坐标系下的“斜率”为 在仿射坐标系下的“斜率”为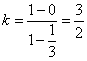 ,故直线 ,故直线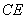 在仿射坐标系下的“点斜式”方程为 在仿射坐标系下的“点斜式”方程为 ②.解①②得 ②.解①②得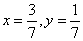 ,则点 ,则点 的坐标为 的坐标为 ,所以 ,所以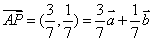 ,故选 ,故选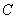 . .

图2
三、仿射坐标系下的线性规划问题
下面在类比思想的引领下用仿射坐标系下的线性规划解法解一类向量创新问题.
例5(2011南昌联考)已知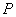 是 是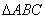 内任一点(不包括三角形边上的点),且满足 内任一点(不包括三角形边上的点),且满足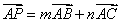 ,则 ,则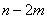 的取值范围是__ 的取值范围是__
解 以 为原点以 为原点以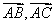 作为 作为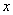 轴 轴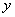 轴上的单位向量建立仿射坐标系如图3所示,设 轴上的单位向量建立仿射坐标系如图3所示,设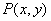 则 则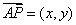 ,又因为 ,又因为 ,于是有 ,于是有 ,则 ,则 ,设 ,设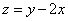 即 即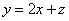 该方程表示直线 该方程表示直线 ,当直线 ,当直线 过点 过点 时, 时, ,当直线 ,当直线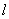 过点 过点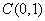 时, 时,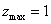 。因 。因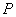 是 是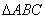 内任一点,所以 内任一点,所以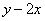 的取值范围是 的取值范围是 . .

图3
例6(2009年高考安徽理科第14题)如图4,给定两个长度为1的两个向量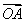 和 和 ,它们的夹角为 ,它们的夹角为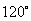 ,点 ,点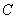 在以 在以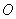 为圆心的圆弧 为圆心的圆弧 上变动,若 上变动,若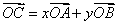 ,其中 ,其中 ,则 ,则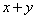 的最大值是 的最大值是
 
图4 图5
解 以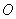 为原点以 为原点以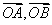 作为 作为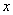 轴 轴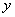 轴上的单位向量建立仿射坐标系如图5所示.设 轴上的单位向量建立仿射坐标系如图5所示.设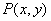 则 则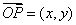 ,又因为 ,又因为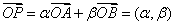 ,于是有 ,于是有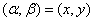 ,则 ,则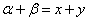 ,设 ,设 该方程表示直线 该方程表示直线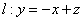 .而直线 .而直线 的方程是 的方程是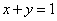 ,所以 ,所以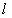 平行于 平行于 ,当直线 ,当直线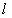 与圆弧 与圆弧 相切于点 相切于点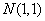 时,直线 时,直线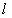 在 在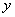 轴上的截距 轴上的截距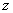 最大, 最大, 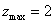 ,故 ,故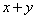 的最大值是2. 的最大值是2.
例7(2011年唐山市)在平行四边形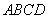 中, 中, 分别为 分别为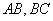 的中点,记 的中点,记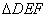 三边及其内部组成的区域为 三边及其内部组成的区域为 , , ,当点 ,当点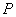 在 在 上运动时, 上运动时,
则 的最大值为 的最大值为
解 以 为原点以 为原点以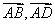 作为 作为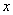 轴 轴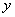 轴上的单位向量建立仿射坐标系如图6所示,设 轴上的单位向量建立仿射坐标系如图6所示,设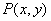 则 则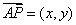 ,又因为 ,又因为 ,于是有 ,于是有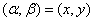 ,则 ,则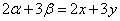 ,设 ,设 即 即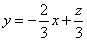 该方程表示直线 该方程表示直线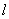 ,因为直线 ,因为直线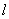 的“斜率” 的“斜率” ,所以当直线 ,所以当直线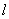 过点 过点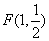 时, 时,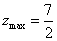 。 。

图6
例8如图7,正六边形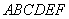 中, 中, 是 是 内(包括边界)的动点,设 内(包括边界)的动点,设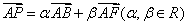 ,则 ,则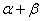 的取值范围是__ 的取值范围是__
 
图7 图8
解 如图8,以 为原点以 为原点以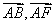 作为 作为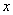 轴 轴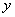 轴上的单位向量建立仿射坐标系.设 轴上的单位向量建立仿射坐标系.设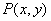 则 则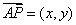 ,又因为 ,又因为 ,于是有 ,于是有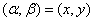 ,则 ,则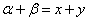 ,设 ,设 该方程表示的直线 该方程表示的直线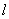 与直线 与直线 平行.由图2知, 平行.由图2知, ,当直线 ,当直线 与 与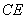 重合即直线 重合即直线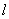 过点 过点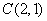 时在 时在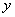 轴上的截距 轴上的截距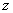 最小, 最小,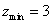 ;当直线 ;当直线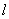 过点 过点 时在 时在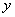 轴上的截距 轴上的截距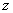 最大, 最大,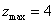 ,故 ,故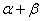 的取值范围是 的取值范围是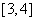 . .
例9(06年湖南高考题改编)如图9, ,点在由射线 ,点在由射线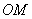 线段 线段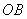 及 及 的延长线围成的阴影区域内)不含边界)运动,且 的延长线围成的阴影区域内)不含边界)运动,且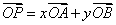 .(1)实数对 .(1)实数对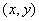 可以是( ) 可以是( )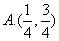 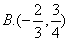 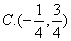 
(2)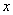 的取值范围是__;当 的取值范围是__;当 时, 时,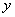 的取值范围是__ 的取值范围是__
解(特殊化)特别地,取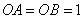 且 且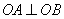 并建立直角坐标系如图1所示,则 并建立直角坐标系如图1所示,则 .又直线 .又直线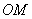 的方程为 的方程为 ,直线 ,直线 的方程为 的方程为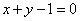 ,因点 ,因点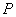 在阴影区域内,所以 在阴影区域内,所以 ,经检验知,(1)应选 ,经检验知,(1)应选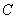 . .
(2)因直线 与直线 与直线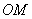 和直线 和直线 交点的纵坐标分别为 交点的纵坐标分别为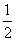 和 和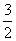 ,由图12知,当 ,由图12知,当 时, 时,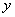 的取值范围是 的取值范围是 . .
 
图9 图10
坐标法是数学方法中最重要的方法之一,解析几何的核心思想是“坐标法”,坐标法就是数形结合思想的体现.综上所述,构建仿射坐标系解决向量共线、向量线性表示以及线性规划等有关问题具有独特的解题功能,方法坐标化运算化、解法直观快捷,学生容易掌握便于运用“仿射坐标系”是在学生熟悉的“直角坐标系”相关知识和思想方法的类比拓展,符合“最近发展处”的理论要求.构建仿射坐标系解题,同时也是培养学生类比推理能力、知识思想方法迁移能力和创新思维能力的良好载体.
(责任编辑:admin)
|
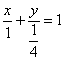 即
即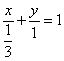 即
即
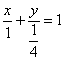 即
即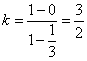 ,故直线
,故直线






 ,经检验知,(1)应选
,经检验知,(1)应选
