错解剖析得真知（二）
http://www.newdu.com 2025/05/19 11:05:56 人民教育出版社 佚名 参加讨论
错解剖析得真知（二） 第二章 函数概念与基本初等函数 §2.1 映射、函数、反函数 一、知识导学 1.映射：一般地，设A、B两个集合，如果按照某种对应法则  ，对于集合A中的任何一个元素，在集合B中都有唯一的元素和它对应，那么这样的单值对应叫做集合A到集合 B的映射，记作f：A→B.(包括集合A、B及A到B的对应法则)2.函数： 设A，B都是非空的数集，如果按某种对应法则  ，对于集合A中每一个元素 ，在集合B中都有唯一的元素和它对应，且B中每一个元素都有原象，这样的对应叫做从集合A到集合 B的一个函数，记作  .其中所有的输入值 组成的集合A称为函数定义域.对于A中的每一个 ，都有一个输出值 与之对应，我们将所有输出值组成的集合称为函数的值域.3.反函数：一般地，设函数y=f(x)(x∈A)的值域是C，根据这个函数中x,y 的关系，用y把x表示出来，得到x=f-1(y) . 若对于y在C中的任何一个值，通过x在A中都有唯一的值和它对应，那么x=f-1(y)就表示y是自变量，x是自变量y的函数，这样的函数 叫做函数y=f(x)(x∈A)的反函数，记作x=f-1(y). 我们一般用x表示自变量，用y 表示函数，为此我们常常对调函数x=f-1(y)中的字母x,y，把它改写成y=f-1(x) 反函数y=f-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域. 二、疑难知识导析 1.对映射概念的认识 (1)  与  是不同的，即  与  上有序的.或者说：映射是有方向的，(2) 输出值的集合是集合B的子集.即集合B中可能有元素在集合A中找不到对应的输入值.集合A中每一个输入值，在集合B中必定存在唯一的输出值.或者说：允许集合B中有剩留元素；允许多对一，不允许一对多. (3)集合A，B可以是数集，也可以是点集或其它类型的集合. 2.对函数概念的认识 （1）对函数符号  的理解知道 y=与 的含义是一样的，它们都表示  是  的函数，其中  是自变量，是函数值，连接的纽带是法则 .是单值对应.(2)注意定义中的集合 A，B都是非空的数集,而不能是其他集合； （3）函数的三种表示法：解析法，列表法，和图象法. 3.对反函数概念的认识 （1）函数y= 只有满足是从定义域到值域上一一映射，才有反函数；（2）反函数的定义域和值域分别是原函数的值域和定义域，因此反函数的定义域一般不能由其解析式来求，而应该通过原函数的值域而得. （3）互为反函数的函数有相同的单调性，它们的图象关于y=x对称. 三、经典例题导讲 [例1]设M＝｛a，b，c｝，N＝｛－2,0,2｝,求（1）从M到N的映射种数； （2）从M到N的映射满足 (a)>(b)≥f(c),试确定这样的映射的种数.错解：（1）由于M＝｛a，b，c｝，N＝｛－2,0,2｝，结合映射的概念，有 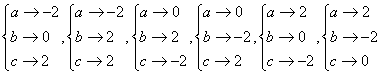 ，共6个映射(2)由（1）得满足条件的映射仅有 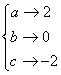 一种情况错因：没有找全满足条件的映射个数，关健是对概念认识不清 正解：（1）由于M＝｛a，b，c｝，N＝｛－2,0,2｝，结合映射的概念，有 一共有27个映射 （2）符合条件的映射共有4个 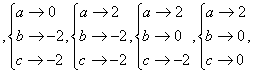 [例2]已知函数 的定义域为[0，1]，求函数 的定义域错解：由于函数 的定义域为[0，1]，即 ， ∴ 的定义域是[1，2]错因：对函数定义域理解不透，不明白 与 定义域之间的区别与联系，其实在这里只要明白：中取值的范围与中式子 的取值范围一致就好了.正解：由于函数 的定义域为[0，1]，即∴满足  ，∴的定义域是[－1，0][例3]已知：   ，求 .错解：∵ ，∴ 故  ，∴＝3－3＝0.错因：没有理解分段函数的意义， 的自变量是3，应代入 中去，而不是代入－5中，只有将自变量化为不小于6的数才能代入解析式求解.正解：∵ ，∴ ＝ ＝ ＝7-5＝2 [例4]已知 的反函数是 ，如果与的图象有交点，那么交点必在直线 上，判断此命题是否正确？ 错解：正确 错因：对互为反函数的图象关于直线 对称这一性质理解不深，比如函数 的图象的交点中，点 不在直线上，由此可以说明“两互为反函数图象的交点必在直线上”是不正确的.[例5]求函数  ， 的值域.错解：  又 ， 的值域是 错因:对函数定义中，输入定义域中每一个x值都有唯一的y值与之对应，错误地理解为x的两端点时函数值就是y的取值范围了. 正解：配方，得  ∵ ，对称轴是 ∴当时，函数取最小值为 2， 的值域是 [例6]已知  ，求函数 的解析式.错解：由已知得   即 ，∴  错因：将函数 错误地认为是的反函数，是由于对函数表达式理解不透彻所致，实际上与并不是互为反函数，一般地应该由先求，再去得到.正解：因为 的反函数为＝ ，所以 ＝ ＝ [例7]根据条件求下列各函数的解析式： （1）已知 是二次函数，若 ，求.（2）已知  ，求（3）若 满足 求解：（1）本题知道函数的类型，可采用待定系数法求解 设 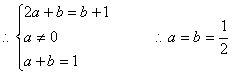＝ 由于 得 ，又由  ，∴ 即   因此：＝ (2)本题属于复合函数解析式问题，可采用换元法求解  设 ∴ ＝ （ ）（3）由于  为抽象函数，可以用消参法求解用  代可得： 与  联列可消去  得：＝ .点评：求函数解析式（1）若已知函数 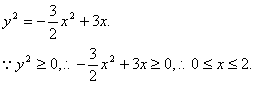的类型，常采用待定系数法；（2）若已知 表达式，常采用换元法或采用凑合法；（3）若为抽象函数，常采用代换后消参法.[例8] 已知  ，试求 的最大值.分析：要求 的最大值，由已知条件很快将变为一元二次函数 然后求极值点的值，联系到 ，这一条件，既快又准地求出最大值.解 由  得 又   当时，有最大值，最大值为 点评：上述解法观察到了隐蔽条件，体现了思维的深刻性.大部分学生的作法如下： 由 得    当 时，取最大值，最大值为 这种解法由于忽略了 这一条件，致使计算结果出现错误.因此，要注意审题，不仅能从表面形式上发现特点，而且还能从已知条件中发现其隐蔽条件，既要注意主要的已知条件，又要注意次要条件，甚至有些问题的观察要从相应的图象着手，这样才能正确地解题..[例9]设 是R上的函数，且满足 并且对任意的实数 都有 ，求的表达式.解法一：由 ，设 ，得  ，所以＝ 解法二：令  ，得 即  又将  用代换到上式中得＝点评：所给函数中含有两个变量时，可对这两个变量交替用特殊值代入，或使这两个变量相等代入，再用已知条件，可求出未知的函数.具体取什么特殊值，根据题目特征而定. 四、典型习题导练 1. 已知函数f(x)，x∈F，那么集合{(x，y)|y=f(x)，x∈F}∩{(x，y)|x=1｝中所含元素的个数是（ ） A.0 B.1 C.0或1 D.1或2 2.对函数  作代换x=g(t)，则总不改变f(x)值域的代换是( ) A. B. C.g(t)=(t－1)2 D.g(t)=cost 3.方程f(x,y)=0的曲线如图所示，那么方程f(2－x,y)=0的曲线是 ( ) 
4.（06年高考全国II）函数f(x)＝的最小值为 A．190 B.171 C.90 D.45 5. 若函数f(x)=  (x≠ )在定义域内恒有f［f(x)］=x,则m等于( )A.3 B.  C.－ D.－36.已知函数  满足： ， ，则 .7.已知函数f(x)满足f(logax)=  (其中a>0,a≠1,x>0),求f(x)的表达式.8.已知函数 是函数 （ R）的反函数，函数 的图象与函数 的图象关于直线y＝x－1成轴对称图形，记 ＝+.（1）求函数F（x）的解析式及定义域； （2）试问在函数F（x）的图象上是否存在两个不同的点A、B，使直线AB恰好与y轴垂直？若存在，求出A、B两点的坐标；若不存在，说明理由. (责任编辑：admin) |
- 上一篇：两圆公共弦所在直线方程与切线长相等
- 下一篇：浅谈高中数学不等式的恒成立问题