两圆公共弦所在直线方程与切线长相等_高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

两圆公共弦所在直线方程与切线长相等

http://www.newdu.com 2025/05/19 11:05:18 人民教育出版社佚名参加讨论

    两圆公共弦所在直线方程与切线长相等
    四川省筠连县中学　邓　敬
    过圆和圆交点的圆系方程：（为参数，且）.
    当时，上式可化为过两圆公共弦所在直线方程：

    【实质】：将两圆方程相减可得两圆公共弦所在直线方程.
    下面介绍几个有关公共弦所在直线方程的重要结论，并举例运用，以加深学生对其该知识点的理解和掌握.
    1.若两圆相交，则方程为它们公共弦所在直线方程.
    【例1】：（新课标人教版A必修二，P133，习题4.2，A组9题）求圆与圆的公共弦长.
    【解析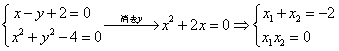】：设两圆交于两点，将两圆方程相减可得公共弦所在直线方程：.
    再由
    再由弦长公式得：.
    当然，此题解法很多，该解法重点体现两圆公共弦所在直线方程的应用，其他解法在这里就不再遨述.
    同题型还有（新课标人教版A必修二，P144，复习参考题A组4题）求圆与圆的公共弦长.
    此题解答可参照例1.
    2.两圆外一动点P，向两相交圆所引切线长相等，则方程是P点的轨迹方程.
    【例2-1】：圆与圆外一动点P，向两圆所引切线长相等，则动点P的轨迹方程为

    　　　　　　　　　　　

    【解析】：由切线长定理可知：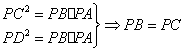

    所以P在两圆的公共弦所在直线上.
    即P点的轨迹为（P在两圆外）.
    【例2-2】：已知和，在平面上找一点P，过P点引两圆切线并使他们的长都等于.
    【说明】：圆外一点，则向圆引切线长满足：.
    【解析】：如图所示，P点是两圆公共弦所在直线与以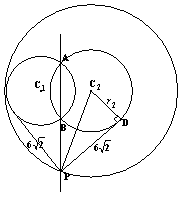（或）为圆心，以（或）为半径的圆的交点.
    　　　　　　　　　　　　　　

    ∴设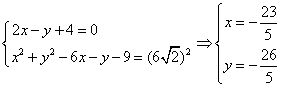，依题意可得：
    或
    ∴P的坐标是或.
    【例2-3】：（新课标人教版A必修二，P144，复习参考题，A组6题），已知圆和圆关于直线对称，求直线方程.
    【解析】：由题意可知两圆相交，对称轴是两圆的中垂线.
    将两圆方程相减可得到其对称轴方程：.
    3.一动点P，向两相外切的圆所引切线长相等，则方程是P点的轨迹方程.
    【例3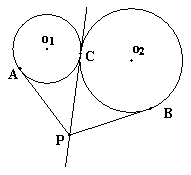】：已知与相外切，两圆外一动点P，向两圆所引切线长相等，则P点的轨迹方程.
    【解析】：如图所示，，
    　　　　　　　　　　

    ∴P点的轨迹方程仍为两圆方程之差,即为：.
    4.一动点P，向两相外离的圆所引切线长相等，则方程是P点的轨迹方程.
    两圆外离是将相交两圆的圆心距扩大所致，所以可以进行类比推理.
    【例4-1】：（07四川理15）、已知的方程是，的方程是，由动点向和所引的切线长相等，则动点的轨迹方程是
    【解析】：：圆心，半径；：圆心，半径．两圆外离.
    动点的轨迹由两圆方程相减可得：
    ．
    【例4-2】：（新课标人教版A必修二，P144，复习参考题A组7题）求与圆关于直线对称的圆的方程.
    【注意】：圆C和直线是相外离，所以对称后的两圆位置关系是外离，但是由于与已知圆共弦的圆不能唯一确定，所以通过类比此题不能用公共弦所在直线方程的思路来处理.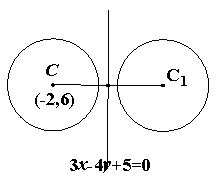
    　　　　　　　　　　　　

    【解析】：圆C圆心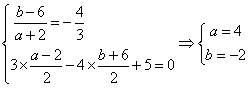（），，设所求圆方程为，直线是两圆连心线的垂直平分线.
    ∴
    ∴所求圆的方程为.
    同类型的题还有（新课标人教版A必修二，P133，习题4.2，A组7题），求与圆C：关于直线L:对称的圆的方程.
    同学们可以参照例题4-2求解.
     (责任编辑：admin)

两圆公共弦所在直线方程与切线长相等

http://www.newdu.com 2025/05/19 11:05:18 人民教育出版社 佚名 参加讨论

http://www.newdu.com 2025/05/19 11:05:18 人民教育出版社佚名参加讨论