斐波那契数列的通项公式推导
http://www.newdu.com 2025/12/23 04:12:54 人民教育出版社 佚名 参加讨论
斐波那契数列的通项公式推导 山西省原平市原平一中 任所怀 做了这些年的数学题,我时常有这样的感受。一个新的数学题初次接触时,会觉得这个题的解题技巧很妙,甚至有点非夷所思,但如果把同类型问题多做几个,你就会发现原来所谓的技巧,其实是一种再正常不过的想法,是一种由已知到未知的必然之路。这样我们就由解题的技巧而转化到了通解通法,进一步就会形成解题的思想,所以我对于数学爱好者建议,做题时要把同类型题多种总结和分析,这样你的数学才会有长足的进步。 下面我们就由递推推导通项的问题,进行对比分析。 例1 在数列 分析:此题可分两步来进行,首先由 解: 设 于是有 设 由累加法可得 因为 于是有 总结:上面的求解过程实质,求是一个把已知条件逐步化简的过程,由相邻三项的递推关系化为相邻两项的递推关系,进一步求出通项公式。 下面我们来研究一下著名的斐波那契数列的通项。 已知数列 解:首先我们要构造一个等比数列,于是设 则有 则由已知 对照(1)(2)两式得 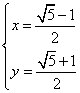 或 或 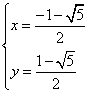 。 。我们取前一解,就会有 设 所以数列 所以 再次构造等比数列,设 则有 对照(3)式,可得 于是有 设 所以有 作者简介:任所怀,性别男,山西省原平市原平一中数学教师。生于1973年9月10日,主要致力于中学数学教学研究。 (责任编辑:admin) |
- 上一篇:错解剖析得真知(三)
- 下一篇:两圆公共弦所在直线方程与切线长相等