错解剖析得真知(三)
http://www.newdu.com 2025/05/19 11:05:56 人民教育出版社 佚名 参加讨论
错解剖析得真知(三) §2.2函数的性质 一、知识导学 1.函数的单调性: (1)增函数:一般地,设函数 (2)减函数:一般地,设函数 (3)单调性(单调区间)如y=f(x)在某个区间上是增函数或减函数,那么就说函数f(x)在这区间上具有单调性,这一区间叫做函数y=f(x)的单调区间. 2.函数的奇偶性: (1)奇函数:一般地,如果对于函数f(x)的定义域内的任意一个x,都有f(-x) =-f(x),那么函数f(x)就叫做奇函数. (2)一般地,如果对于函数f(x)的定义域内的任意一个x,都有f(-x) =f(x),那么函数f(x)就叫做偶函数. (3)如果函数f(x)是奇函数或偶函数,那么就说f(x)具有奇偶性. 3.函数的图象:将自变量的一个值x0作为横坐标,相应的函数值f(x0)作为纵坐标,就得到平面内的一个点(x0,f(x0)),当自变量取遍函数定义域内的每一个值时,就得到一系列这样的点,所有这些点的集合(点集)组成的图形就是函数y=f(x)的图象. 二、疑难知识导析 1. 对函数单调性的理解, 函数的单调性一般在函数的定义域内的某个子区间上来讨论,函数y=f(x)在给定区间上的单调性,反映了函数在区间上函数值的变化趋势,是函数在区间上的整体性质,但不一定是函数在定义域上的整体性质.函数的单调性是对某个区间而言的,所以要受到区间的限制. 2.对函数奇偶性定义的理解,不能只停留在f(-x)=f(x)和f(-x)=-f(x)这两个等式上,要明确对定义域内任意一个x,都有f(-x)=f(x),f(-x)=-f(x)的实质:函数的定义域关于原点对称.这是函数具备奇偶性的必要条件.稍加推广,可得函数f(x)的图象关于直线x=a对称的充要条件是对定义域内的任意x,都有f(x+a)=f(a-x)成立.函数的奇偶性是其相应图象的特殊的对称性的反映. 这部分的难点是函数的单调性和奇偶性的综合运用.根据已知条件,调动相关知识,选择恰当的方法解决问题,是对学生能力的较高要求. 3. 用列表描点法总能作出函数的图象,但是不了解函数本身的特点,就无法了解函数图象的特点,如二次函数图象是抛物线,如果不知道抛物线的顶点坐标和存在着对称轴,盲目地列表描点是很难将图象的特征描绘出来的. 三、经典例题导讲 [例1]判断函数 错解: 错因:概念不清,导致判断错误.这是一个复合函数,而复合函数的单调性(或单调区间),仍是从基础函数的单调性(或单调区间)分析,但需注意内函数与外函数的单调性的变化.当然这个函数可化为 正解: 令 ∴ [例2]判断函数 错解:∵ ∴ ∴ 错因:对函数奇偶性定义实质理解不全面.对定义域内任意一个x,都有f(-x)=f(x),f(-x)=-f(x)的实质是:函数的定义域关于原点对称.这是函数具备奇偶性的必要条件. 正解: 即函数的定义域是{ [例3] 判断 错解:∵ ∴ 所以该函数既不是奇函数也不是偶函数 错因:对数运算公式不熟悉,或者说奇偶性的判别方法不灵活.定义中f(-x)=-f(x) f(-x)=f(x),也可改为研究f(-x)+f(x) =0 ,f(-x)-f(x)=0是否成立. 正解:方法一:∵ = ∴ 方法二:∵ = [例4]函数y= 错解:因为函数 错因:在求单调性的过程中注意到了复合函数的单调性研究方法,但没有考虑到函数的单调性只能在函数的定义域内来讨论,从而忽视了函数的定义域,导致了解题的错误. 正解:y= [例5] 已知奇函数f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,求x的取值范围. 错解:∵f(x)是奇函数,∴f(x-3)<-f(x2-3)= f (3-x2),又f(x)在(-3,3)上是减函数, ∴x-3>3-x2,即x2+x-6>0 解得x>2或x<-3 又 f(x)是定义在(-3,3)上的函数, 所以2<x<3 错因:只考虑到奇函数与单调性,而没有正确理解函数的定义域. 正解:由 又∵f(x)是奇函数,∴f(x-3)<-f(x2-3)=f(3-x2),又f(x)在(-3,3)上是减函数, ∴x-3>3-x2,即x2+x-6>0,解得x>2或x<-3,综上得2<x< [例6] 作出下列函数的图象(1)y=|x-2|(x+1);(2) 分析:显然直接用已知函数的解析式列表描点有些困难,除去对其函数性质分析外,我们还应想到对已知解析式进行等价变形.在变换函数解析式中运用了转化变换和分类讨论的思想. 所以 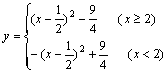 这是分段函数,每段函数图象可根据二次函数图象作出(见图) 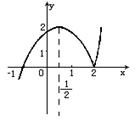 (2)当x≥1时,lgx≥0,y 当0<x<1时,lgx<0, 所以 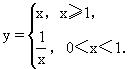 这是分段函数,每段函数可根据正比例函数或反比例函数作出.(见图) 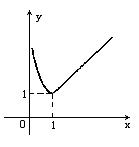 点评:作不熟悉的函数图象,可以变形成基本函数再作图,但要注意变形过程是否等价,要特别注意x,y的变化范围.因此必须熟记基本函数的图象.例如:一次函数、反比例函数、二次函数、指数函数、对数函数,及三角函数、反三角函数的图象. [例7]若f(x)= 解:设 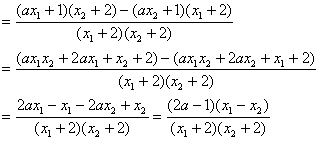 由f(x)= 点评:有关于单调性的问题,当我们感觉陌生,不熟悉或走投无路时,回到单调性的定义上去,往往给我们带来“柳暗花明又一村”的感觉. [例8] 已知函数f(x)在(-1,1)上有定义,f( (1)f(x)为奇函数;(2)f(x)在(-1,1)上单调递减 解:证明:(1)由f(x)+f(y)=f( (2)先证f(x)在(0,1)上单调递减. 令0<x1<x2<1,则f(x2)-f(x1)=f(x2)+f(-x1)=f( ∵0<x1<x2<1,∴x2-x1>0,1-x1x2>0,∴ 又(x2-x1)-(1-x2x1)=(x2-1)(x1+1)<0 ∴x2-x1<1-x2x1, ∴0< 即f(x2)<f(x1). ∴f(x)在(0,1)上为减函数,又f(x)为奇函数且f(0)=0. ∴f(x)在(-1,1)上为减函数. 点评:本题知识依托:奇偶性及单调性定义及判定、赋值法及转化思想.对函数的奇偶性、单调性的判定以及运算能力和逻辑推理能力要求较高. 如果“赋值”不够准确,运算技能不过关,结果很难获得. 对于(1),获得f(0)的值进而取x=-y是解题关键;对于(2),判定 四、典型习题导练 1.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了,再走余下的路,下图中y轴表示离学校的距离,x轴表示出发后的时间,则适合题意的图形是( ) 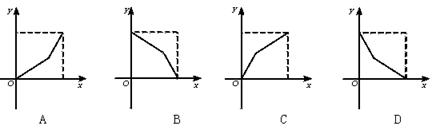 2. (05年高考重庆卷) 若函数 A. 3. (05年高考江西卷)若函数 4. (05年高考辽宁卷)已知 A. 5.已知 6. 已知函数f(x)的定义域为R,且对m、n∈R,恒有f(m+n)=f(m)+f(n)-1,且f(- 当x>- (1)求证:f(x)是单调递增函数; (2)试举出具有这种性质的一个函数,并加以验证. 7.已知函数y=f(x)= (1)试求函数f(x)的解析式; (2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由. (责任编辑:admin) |
- 上一篇:错解剖析得真知(四)
- 下一篇:斐波那契数列的通项公式推导