错解剖析得真知(四)
http://www.newdu.com 2025/12/23 06:12:39 人民教育出版社 佚名 参加讨论
错解剖析得真知(四) §2.3 基本初等函数 一、知识导学 1. 二次函数的概念、图象和性质. (1)注意解题中灵活运用二次函数的一般式 二次函数的顶点式 二次函数的坐标式 (2)解二次函数的问题(如单调性、最值、值域、二次三项式的恒正恒负、二次方程根的范围等)要充分利用好两种方法:配方、图象,很多二次函数都用数形结合的思想去解. ① M(x1,0)N(x2,0),|MN|=| x1- x2|= ② 二次函数在闭区间上必有最大值和最小值,它只能在区间的端点或二次函数的顶点处取得. 2.指数函数 (1)有理指数幂的意义、幂的运算法则: ① 对数的概念及其运算性质、换底公式. (2)指数函数的图象、单调性与特殊点.对数函数的图象、单调性与特殊点. ①指数函数图象永远在x轴上方,当a>1时,图象越接近y轴,底数a越大;当0<a<1时,图象越接近y轴,底数a越小. ②对数函数的符号常受到底数和真数的范围的制约,注意对底数a的讨论. ③当a>1时,图象越接近x轴,底数a越大; 当0<a<1时,图象越接近x轴,底数a越小. 3.幂函数 结合函数y=x,y=x2 ,y=x3,y= ① 注意 ② ③当x>1时,指数大的图象在上方. 二、疑难知识导析 1.二次函数在区间上最值的求解要注意利用二次函数在该区间上的图象.二次函数的对称轴与区间的位置通常有三种情况:(1)定义域区间在对称轴的右侧;(2)定义域区间在对称轴的左侧;(3)对称轴的位置在定义域区间内 2.幂的运算性质、对数的运算性质的运用,要注意公式正确使用.会用语言准确叙述这些运算性质防止出现下列错误: (1)式子 (2) 3.利用指数函数的性质解题,一定要注意底数的取值. 4.函数 5.对数函数 6.幂函数 (1)当 三、经典例题导讲 [例1]已知 错解:∵ ∴ 错因:因对性质不熟而导致题目没解完. 正解:∵ ∴ 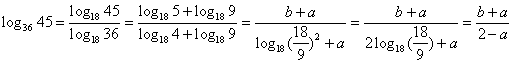 [例2]分析方程 错解:由于方程 故需满足  ,所以充要条件是 ,所以充要条件是 错因:上述解法中,只考虑到二次函数与x轴交点坐标要大于1,却忽视了最基本的的前题条件,应让二次函数图象与x轴有交点才行,即满足△≥0,故上述解法得到的不是充要条件,而是必要不充分条件. 正解:充要条件是  [例3]求函数 错解:令 ∴当t≥6,即x≥1时,y为关于t的增函数, 当t≤6,即x≤1时,y为关于t的减函数 ∴函数 错因:本题为复合函数,该解法未考虑中间变量的取值范围. 正解:令 ∴当t≥6,即x≥1时,y为关于t的增函数, 当t≤6,即x≤1时,y为关于t的减函数 ∴函数 [例4]已知 错解:∵ ∴ 错因:错因:解题中虽然考虑了对数函数与一次函数复合关系,却忽视了数定义域的限制,单调区间应是定义域的某个子区间,即函数应在[0,1]上有意义. 正解:∵ ∴ 又由于 综上可知所求的取值范围是1< [例5]已知函数 (1)当 (2)是否存在这样的实数 分析:函数 解:(1)由假设, 显然,函数g(x)= ∴ (2)假设存在这样的实数 ∴ 当 点评:本题为探索性问题,应用函数、方程、不等式之间的相互转化,存在性问题一般的处理方法是先假设存在,结合已知条件进行推理和等价转化,若推出矛盾,说明假设不成立.即不存在,反之没有矛盾,则问题解决. [例6]已知函数f(x)= 分析:参数深含在一个复杂的复合函数的表达式中,欲直接建立关于 解: ∴ 1+2x+4x·a>0, a> 当x∈(-∞, 1]时, y= ∴ y= ∴ a>- 点评:发掘、提炼多变元问题中变元间的相互依存、相互制约的关系、反客为主,主客换位,创设新的函数,并利用新函数的性质创造性地使原问题获解,是解题人思维品质高的表现.本题主客换位后,利用新建函数y= [例7]若 解:∵幂函数 ∴根据 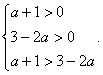 ① ① 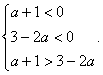 ② ② 解三个不等式组:①得 ∴ 点评:幂函数 [例8] 已知a>0 且a≠1 ,f (log a x ) = (1)求f(x); (2)判断f(x)的奇偶性与单调性; (3)对于f(x) ,当x ∈(-1 , 1)时 , 有f( 1-m ) +f (1- m2 ) < 0 ,求m的集合M . 分析:先用换元法求出f(x)的表达式;再利用有关函数的性质判断其奇偶性和单调性;然后利用以上结论解第三问. 解:(1)令t=logax(t∈R),则  f(x)在R上都是增函数. 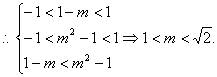 点评:对含字母指数的单调性,要对字母进行讨论.对本例的③不需要代入f(x)的表达式可求出m的取值范围,请同学们细心体会. 四、典型习题导练 1. 函数 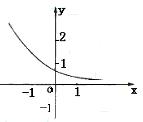 A. C. (05年高考福建试题) 2.已知2lg(x-2y)=lgx+lgy,则 A.1 B.4 C.1或4 D.4 或 8 3.方程 A.0 B.1 C.2 D.3 4.函数f(x)与g(x)=( A. 5.图中曲线是幂函数y=xn在第一象限的图象,已知n可取±2,± 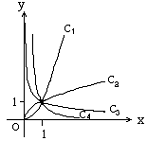 A.-2,- C. - 6. 求函数y = log 2 (x2 -5x+6) 的定义域、值域、单调区间. 7. 若x满足 8.已知定义在R上的函数 (1)如果 (2)当 (责任编辑:admin) |
- 上一篇:错解剖析得真知(五)
- 下一篇:错解剖析得真知(三)