错解剖析得真知(十三)
http://www.newdu.com 2025/12/23 02:12:55 人民教育出版社 佚名 参加讨论
错解剖析得真知(十三) §5.2简单的线性规划 一、知识导学 1. 目标函数: P =2x+y是一个含有两个变 量 x 和y 的 函数,称为目标函数. 2.可行域:约束条件所表示的平面区域称为可行域. 3. 整点:坐标为整数的点叫做整点. 4.线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题.只含有两个变量的简单线性规划问题可用图解法来解决. 5. 整数线性规划:要求量取整数的线性规划称为整数线性规划. 二、疑难知识导析 线性规划是一门研究如何使用最少的人力、物力和财力去最优地完成科学研究、工业设计、经济管理中实际问题的专门学科.主要在以下两类问题中得到应用:一是在人力、物力、财务等资源一定的条件下,如何使用它们来完成最多的任务;二是给一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务. 1.对于不含边界的区域,要将边界画成虚线. 2.确定二元一次不等式所表示的平面区域有多种方法,常用的一种方法是“选点法”:任选一个不在直线上的点,检验它的坐标是否满足所给的不等式,若适合,则该点所在的一侧即为不等式所表示的平面区域;否则,直线的另一侧为所求的平面区域.若直 线 不 过 原点,通 常 选 择 原 点 代入检验. 3. 平 移 直 线 y=-kx +P时,直线必须经过可行域. 4.对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形的顶点. 5.简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的:(1)寻找线性约束条件,线性目标函数;(2)由二元一次不等式表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解. 三、经典例题导讲 [例1] .画出不等式组 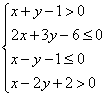 表示的平面区域. 表示的平面区域.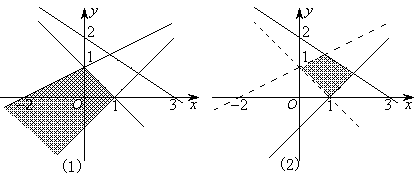 错解:如图(1)所示阴影部分即为不等式组 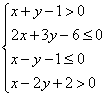 表示的平面区域. 表示的平面区域.错因一是实虚线不清,二是部分不等式所表示的平面区域弄错了. 正解:如图(2)所示阴影部分即为不等式组 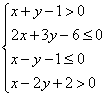 表示的平面区域. 表示的平面区域.[例2] 已知1 错解:由于 1 2 ①+② 得3 ①×(-1)+② 得:0 ③×2+④×(-1)得. 3 错因:可行域范围扩大了. 正解:线性约束条件是: 令z=4x-2y, 画出可行域如图所示,  由 由 [例3] 已知 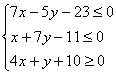 ,求x2+y2的最值. ,求x2+y2的最值.错解:不等式组 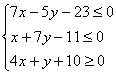 表示的平面区域如图所示 表示的平面区域如图所示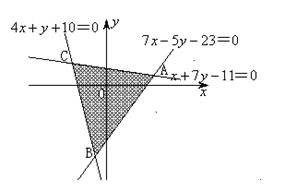 令z= x2+y2 由 此时z=x2+y2=42+12=17, 由 此时z=x2+y2=(-1)2+(-6)2=37, 由 此时z=x2+y2=(-3)2+22=13, 错因:误将求可行域内的点到原点的距离的平方的最值误认为是求三点A、B、C到原点的距离的平方的最值. 正解:不等式组 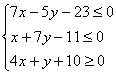 表示的平面区域如图所示 表示的平面区域如图所示令z= x2+y2,则z即为点(x,y)到原点的距离的平方. 由 此时z=x2+y2=42+12=17, 由 此时z=x2+y2=(-1)2+(-6)2=37, 由 此时z=x2+y2=(-3)2+22=13, 而在原点处, [例4]某家具厂有方木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m3,五合板1m2,出售一张书桌可获利润80元,出售一个书橱可获利润120元.如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使得利润最大? 分析: 数据分析列表
设生产书桌x张,书橱y张,利润z元,则约束条件为  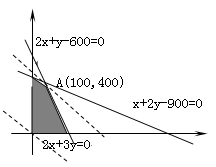 目标函数z=80x+120y 作出上可行域: 作出一组平行直线2x+3y=t, 此直线经过点A(100,400)时,即合理安排生产,生产书桌100张,书橱400张,有最大利润为 zmax=80×100+400×120=56000(元) 若只生产书桌,得0<x≤300,即最多生产300张书桌,利润为 z=80×300=24000(元) 若只生产书橱,得0<y≤450,即最多生产450张书橱,利润为 z=120×450=54000(元) 答:略 [例5]某钢材厂要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表:
每张钢板的面积,第一种为1m2,第二种为2 m2,今需要A、B、C三种规格的成品各12、15、27块,请你们为该厂计划一下,应该分别截这两种钢板多少张,可以得到所需的三种规格成品,而且使所用钢板的面积最小?只用第一种钢板行吗? 解:设需要截第一种钢板x张,第二种钢板y张,所用钢板面积为z m2,则 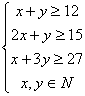 目标函数z=x+2y 目标函数z=x+2y作出可行域如图 作一组平行直线x+2y=t, 由 可得交点 但点 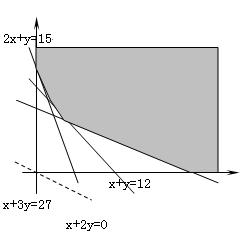 若只截第一种钢板,由上可知x≥27,所用钢板面积最少为z=27(m2);若只截第二种钢板,则y≥15,最少需要钢板面积z=2×15=30(m2).它们都比zmin大,因此都不行. 答:略 [例6]设 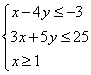 ,求 ,求解:由引例可知:直线 当 当 说明:1.线性目标函数的最大值、最小值一般在可行域的顶点处取得; 2.线性目标函数的最值也可在可行域的边界上取得,即满足条件的最优解有无数多个. 四、典型习题导练 1.画出不等式- 2.画出不等式组 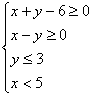 表示的平面区域 表示的平面区域3.求z=3x+5y的最大值和最小值,使式中的x、y满足约束条件 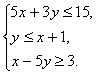 4.某工厂用两种不同原料均可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90千克;若采用乙种原料,每吨成本为1500元,运费400元,可得产品100千克,如果每月原料的总成本不超过6000元,运费不超过2000元,那么此工厂每月最多可生产多少千克产品? 5.某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大? 6.(06年高考广东)在约束条件 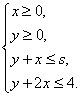 下,当 下,当A.[6,15] B.[7,15] C.[6,8] D.[7,8] §5.3 基本不等式的证明 一、知识导学 1.比较法:比较法是证明不等式的最基本、最重要的方法之一,它是两个实数大小顺序和运算性质的直接应用,比较法可分为差值比较法(简称为求差法)和商值比较法(简称为求商法). (1)差值比较法的理论依据是不等式的基本性质:“a-b≥0 (2)商值比较法的理论依据是:“若a,b∈R+,a/b≥1 2.综合法:利用已知事实(已知条件、重要不等式或已证明的不等式)作为基础,借助不等式的性质和有关定理,经过逐步的逻辑推理,最后推出所要证明的不等式,其特点和思路是“由因导果”,从“已知”看“需知”,逐步推出“结论”.即从已知A逐步推演不等式成立的必要条件从而得出结论B. 3.分析法:是指从需证的不等式出发,分析这个不等式成立的充分条件,进而转化为判定那个条件是否具备,其特点和思路是“执果索因”,即从“未知”看“需知”,逐步靠拢“已知”.用分析法证明书写的模式是:为了证明命题B成立,只需证明命题B1为真,从而有…,这只需证明B2为真,从而又有…,……这只需证明A为真,而已知A为真,故B必为真.这种证题模式告诉我们,分析法证题是步步寻求上一步成立的充分条件. 4.反证法:有些不等式的证明,从正面证不好说清楚,可以从正难则反的角度考虑,即要证明不等式A>B,先假设A≤B,由题设及其它性质,推出矛盾,从而肯定A>B.凡涉及到的证明不等式为否定命题、惟一性命题或含有“至多”、“至少”、“不存在”、“不可能”等词语时,可以考虑用反证法. 5.换元法:换元法是对一些结构比较复杂,变量较多,变量之间的关系不甚明了的不等式可引入一个或多个变量进行代换,以便简化原有的结构或实现某种转化与变通,给证明带来新的启迪和方法.主要有两种换元形式.(1)三角代换法:多用于条件不等式的证明,当所给条件较复杂,一个变量不易用另一个变量表示,这时可考虑三角代换,将两个变量都有同一个参数表示.此法如果运用恰当,可沟通三角与代数的联系,将复杂的代数问题转化为三角问题; (2)增量换元法:在对称式(任意交换两个字母,代数式不变)和给定字母顺序(如a>b>c等)的不等式,考虑用增量法进行换元,其目的是通过换元达到减元,使问题化难为易,化繁为简.如a+b=1,可以用a=1-t,b=t或a=1/2+t,b=1/2-t进行换元. 二、疑难知识导析 1.在用商值比较法证明不等式时,要注意分母的正、负号,以确定不等号的方向. 2.分析法与综合法是对立统一的两个方面,前者执果索因,利于思考,因为它方向明确,思路自然,易于掌握;后者是由因导果,宜于表述,因为它条理清晰,形式简洁,适合人们的思维习惯.但是,用分析法探求证明不等式,只是一种重要的探求方式,而不是一种好的书写形式,因为它叙述较繁,如果把“只需证明”等字眼不写,就成了错误.而用综合法书写的形式,它掩盖了分析、探索的过程.因而证明不等式时,分析法、综合法常常是不能分离的.如果使用综合法证明不等式,难以入手时常用分析法探索证题的途径,之后用综合法形式写出它的证明过程,以适应人们习惯的思维规律.还有的不等式证明难度较大,需一边分析,一边综合,实现两头往中间靠以达到证题的目的.这充分表明分析与综合之间互为前提、互相渗透、互相转化的辩证统一关系.分析的终点是综合的起点,综合的终点又成为进一步分析的起点. 3.分析法证明过程中的每一步不一定“步步可逆”,也没有必要要求“步步可逆”,因为这时仅需寻找充分条件,而不是充要条件.如果非要“步步可逆”,则限制了分析法解决问题的范围,使得分析法只能使用于证明等价命题了.用分析法证明问题时,一定要恰当地用好“要证”、“只需证”、“即证”、“也即证”等词语. 4.反证法证明不等式时,必须要将命题结论的反面的各种情形一一加以导出矛盾. 5.在三角换元中,由于已知条件的限制作用,可能对引入的角有一定的限制,应引起高度重视,否则可能会出现错误的结果.这是换元法的重点,也是难点,且要注意整体思想的应用. 三、经典例题导讲 [例1] 已知a>b(ab 错解: 错因:简单的认为大数的倒数必定小,小数的倒数必定大.正确的结论是:当两数同号时,大数的倒数必定小,小数的倒数必定大. 正解: (1)当a、b同号时,即a>b>0或b<a<0时,则ab>0,b-a<0, (2)当a、b异号时,则a>0,b<0, [例2] 当a、b为两个不相等的正实数时,下列各式中最小的是( ) A. 错解:所以选B. 错因是由于在 正解:由均值不等式 [例3] 已知:a>0 , b>0 , a+b=1,求(a+ )2+(b+ )2的最小值. 错解: (a+ ∴(a+ 错因:上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b= 正解:原式= a2+b2+ = (1-2ab)(1+ 由ab≤( ∴原式≥ ∴(a + [例4] 已知0 < x < 1, 0 < a < 1,试比较 解法一: ∵0 < 1 - x2 < 1, ∴ 解法二: 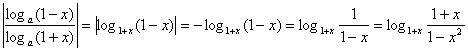 ∵0 < 1 - x2 < 1, 1 + x > 1, ∴ ∴ 解法三:∵0 < x < 1, ∴0 < 1 - x < 1, 1 < 1 + x < 2, ∴ ∴左 - 右 = ∵0 < 1 - x2 < 1, 且0 < a < 1 ∴ ∴ [例5]已知x2 = a2 + b2,y2 = c2 + d2,且所有字母均为正,求证:xy≥ac + bd 证:证法一(分析法)∵a, b, c, d, x, y都是正数 ∴要证:xy≥ac + bd 只需证:(xy)2≥(ac + bd)2 即:(a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd 展开得:a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd 即:a2d2 + b2c2≥2abcd 由基本不等式,显然成立 ∴xy≥ac + bd 证法二(综合法)xy = ≥ 证法三(三角代换法) ∵x2 = a2 + b2,∴不妨设a = xsina, b = xcosa y2 = c2 + d2 c = ysinb, d = ycosb ∴ac + bd = xysinasinb + xycosacosb = xycos(a - b)≤xy [例6] 已知x > 0,求证: 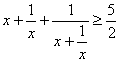 证:构造函数 由 显然 ∵2≤a<b ∴a - b > 0, ab - 1 > 0, ab > 0 ∴上式 > 0 ∴f (x)在 四、典型习题导练 1.比较(a+3)(a-5)与(a+2)(a-4)的大小. 2.已知a,b,c,d都是正数,求证: 3.已知x > 0 , y > 0,2x + y = 1,求证: 4.若 5.若x > 1,y > 1,求证: 6.证明:若a > 0,则 (责任编辑:admin) |
- 上一篇:错解剖析得真知(十四)
- 下一篇:错解剖析得真知(六)