错解剖析得真知（十四）
http://www.newdu.com 2025/05/19 11:05:27 人民教育出版社 佚名 参加讨论
错解剖析得真知（十四） §5.4不等式的应用 一、基础知识导学 1.利用均值不等式求最值：如果a1，a2∈R+，那么  .2.求函数定义域、值域、方程的有解性、判断函数单调性及单调区间，确定参数的取值范围等.这些问题一般转化为解不等式或不等式组，或证明不等式. 3.涉及不等式知识解决的实际应用问题，这些问题大体分为两类：一是建立不等式解不等式；二是建立函数式求最大值或最小值. 二、疑难知识导析 不等式既属数学的基础知识，又是解决数学问题的重要工具，在解决函数定义域、值域、单调性、恒成立问题、方程根的分布、参数范围的确定、曲线位置关系的讨论、解析几何、立体几何中的最值等问题中有广泛的应用，特别是近几年来，高考试题带动了一大批实际应用题问世，其特点是： 1．问题的背景是人们关心的社会热点问题，如“物价、税收、销售收入、市场信息”等，题目往往篇幅较长. 2．函数模型除了常见的“正比例函数、反比例函数、一次函数、二次函数、幂函数、指数函数、对数函数、三角函数、反三角函数”等标准形式外，又出现了以“函数  ”为模型的新的形式. 三 经典例题导讲 [例1]求y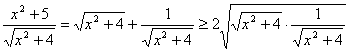=  的最小值.错解：  y= ＝2 y的最小值为2.错因：等号取不到，利用均值定理求最值时“正、定、等”这三个条件缺一不可. 正解：令t=  ,则t ,于是y= 由于当t  时，y= 是递增的，故当t＝2即x=0时，y取最小值 .[例2]m为何值时，方程x2+(2m+1)x+m2－3=0有两个正根. 错解：由根与系数的关系得  ，因此当 时，原方程有两个正根.错因：忽视了一元二次方程有实根的条件，即判别式大于等于0. 正解：由题意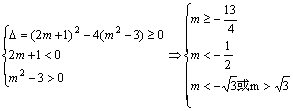：   因此当 时，原方程有两个正根. [例3]若正数x，y满足  ，求xy的最大值．解：由于x，y为正数，则6x，5y也是正数，所以  当且仅当6x=5y时，取“=”号． 因 ，则 ，即 ，所以 的最大值为 .[例4] 已知：长方体的全面积为定值S，试问这个长方体的长、宽、高各是多少时，它的体积最大，求出这个最大值． 分析：经过审题可以看出，长方体的全面积S是定值．因此最大值一定要用S来表示．首要问题是列出函数关系式．设长方体体积为y，其长、宽、高分别为a，b，c，则y=abc．由于a+b+c不是定值，所以肯定要对函数式进行变形．可以利用平均值定理先求出y2的最大值，这样y的最大值也就可以求出来了． 解：设长方体的体积为y，长、宽、高分别是为a，b，c，则 y=abc，2ab+2bc+2ac=S． 而 y2=（abc）2=（ab）（bc）（ac）  当且仅当ab=bc=ac，即a=b=c时，上式取“=”号，y2有最小值 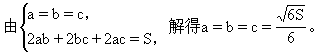  答：长方体的长、宽、高都等于  时体积的最大值为 .说明：对应用问题的处理，要把实际问题转化成数学问题，列好函数关系式是求解问题的关健. 四、典型习题导练 1.某工厂要建造一个长方体无盖贮水池，其容积为4800m3,深为3m，如果池底每1m2的造价为150元，池壁每1m2的造价为120元，问怎样设计水池能使总造价最低，最低总造价是多少元？ 2.证明：通过水管放水，当流速相同时，如果水管截面的周长相等，那么截面是圆的水管比截面是正方形的水管流量大. 3.在四面体P-ABC中，∠APB=∠BPC=∠CPA=90°，各棱长的和为m，求这个四面体体积的最大值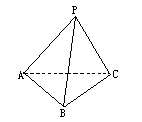．  4. 设函数f(x)=ax2+bx+c的图象与两直线y=x，y=-x，均不相 交，试证明对一切  R都有 .5．青工小李需制作一批容积为V的圆锥形漏斗，欲使其用料最省，问漏斗高与漏斗底面半径应具有怎样的比例？ 6．轮船每小时使用燃料费用(单位：元)和轮船速度(单位：海里／时)的立方成正比．已知某轮船的最大船速是18海里／时，当速度是10海里／时时，它的燃料费用是每小时30元，其余费用(不论速度如何)都是每小时480元，如果甲、乙两地相距1000海里，求轮船从甲地行驶到乙地，所需的总费用与船速的函数关系，并问船速为多少时，总费用最低？ 5.5 推理与证明 一、基础知识导学 1. 推理一般包括合情推理和演绎推理. 2. 合情推理：根据已有的事实和正确的结论（包括定义、公理、定理等）、实验和实践的结果，以及个人的经验和直觉等推测某些结果的推理过程.归纳、类比是合情推理常用的思维方法. 3. 归纳推理：根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理. 4. 归纳推理的一般步骤：⑴通过观察个别情况发现某些相同性质；⑵从已知的相同性质中推出一个明确表达的一般性命题（猜想）. 5. 类比推理：根据两类不同事物之间具有某些类似性，推出其中一类事物具有另一类事物类似的性质的推理. 6. 类比推理的一般步骤：⑴找出两类事物之间的相似性或一致性；⑵从一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）. 7. 演绎推理：根据一般性的真命题导出特殊性命题为真的推理. 8. 直接证明的两种基本方法：分析法和综合法；间接证明的一种基本方法──反证法. 9. 分析法：从原因推导到结果的思维方法. 10. 综合法：从结果追溯到产生这一结果的原因的思维方法. 11. 反证法：判定非q为假，推出q为真的方法. 12. 应用反证法证明命题的一般步骤：⑴分清命题的条件和结论；⑵做出与命题结论相矛盾的假定；⑶由假定出发，应用正确的推理方法，推出矛盾的结果；⑷间接证明命题为真. 13. 数学归纳法：设｛pn｝是一个与自然数相关的命题集合，如果⑴证明起始命题p1成立；⑵在假设pk成立的前提上，推出pk＋1也成立，那么可以断定，｛pn｝对一切正整数成立. 14. 数学归纳法的步骤： （1）证明当  （如 或2等）时，结论正确；（2）假设  时结论正确，证明 时结论也正确．二、疑难知识导析 1.归纳推理是根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理. 而类比推理是根据两类不同事物之间具有某些类似性，推出其中一类事物具有另一类事物类似的性质的推理. 2. 应用反证法证明命题的逻辑依据：做出与命题结论相矛盾的假定，由假定出发，应用正确的推理方法，推出矛盾的结果 3. 数学归纳法是一种证明方法，归纳推理是一种推理方法. 三、经典例题导讲 [例1] {  }是正数组成的数列,其前n项和为 ,并且对于所有的自然数 ,与2的等差中项等于与2的等比中项.(1)写出数列{ }的前3项;(2)求数列{ }的通项公式(写出推证过程);错解：由(1)猜想数列{ }有通项公式=4-2.下面用数学归纳法证明数列{ }的通项公式是=4-2. (∈N).①当 =1时,因为4×1-2=2,又在(1)中已求出 =2,所以上述结论成立.②假设n=k时结论成立,即有  =4 -2.由题意,有 将 =4-2代入上式，得 ，解得 由题意,有  将 代入，化简得 解得  .∴ 这就是说,当n=k+1时,上述结论成立. 根据①、②,上述结论对所有的自然数n成立. 错因在于解题过程中忽视了取值的取舍. 正解：由(1)猜想数列{an}有通项公式an=4n-2. 猜想数列{ }有通项公式=4-2.下面用数学归纳法证明数列{ }的通项公式是=4-2. (∈N).①当 =1时,因为4×1-2=2,又在(1)中已求出=2,所以上述结论成立.②假设n=k时结论成立,即有 =4-2.由题意,有将 =4-2代入上式，得，解得由题意,有 将 代入，化简得解得 .由 ∴这就是说,当n=k+1时,上述结论成立. 根据①、②,上述结论对所有的自然数n成立. [例2] 用数学归纳法证明对于任意自然数  ， 错解：证明：假设当  （ N）时，等式成立，即  ，那么当  时，     这就是说，当 时，等式成立．可知等式对任意 N成立．错因在于推理不严密，没有证明当  的情况．正解：证明：（1）当 时，左式 ，右式 ，所以等式成立．（2）假设当 （ ）时，等式成立，即 ，那么当 时，这就是说，当 时，等式成立．由（1）、（2），可知等式对任意 N成立．[例3] 是否存在自然数  ，使得 对任意自然数，都能被 整除，若存在，求出的最大值，并证明你的结论；若不存在，说明理由．分析 本题是开放性题型，先求出 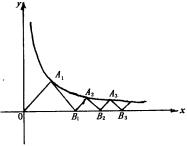 ， ， …再归纳、猜想、证明．解：  ， ， ，…… 猜想，  能被36整除，用数学归纳法证明如下：（1）当 时， ，能被36整除．（2）假设当  ，（N）时， 能被36整除．那么，当 时，   由归纳假设，  能被36整除，当  为自然数时， 为偶数，则 能被36整除．∴  能被36整除，这就是说当 时命题成立．由（1）、（2）对任意  ， 都能被36整除．当 取大于36的自然数时， 不能被整除，所以36为最大．[例4] 设点  是曲线C： 与直线 的交点，过点作直线的垂线交 轴于 ，过点作直线的平行线交曲线C于 ，再过点作的垂线作交X轴于 ，如此继续下去可得到一系列的点 ， ，…， ，…如图，试求的横坐标 的通项公式． 分析 本题并没有指明求 通项公式的方法，可用归纳——猜想——证明的方法，也可以通过寻求与 的递推关系式求的通项公式．解：解法一  与 （ ， ）联立，解得 直线  的方程为 ， 令 ，得 ，所以点 直线  的方程为 与联立，消元得 （），解得 ， 所以点 （ ， ）．直线  的方程为 ，令 ，得 ，所以点 同样可求得点 （ ，0）…… 由此推测 （ ，0），即 用数学归纳法证明 （1）当 时，由点的坐标为（ ，0），即  ，所以命题成立．（2）假设当 时命题成立，即  ，0），则当时，由于直线  的方程为 ，把它与 （，）联立，消去  可得 （），∴  于是  即点  的坐标为（ ， ）．∴ 直线  的方程为 令 得， 即  点的坐标为（ ，0）∴ 当 时，命题成立．解法二 设点 ，的坐标分别为（ ，0）、（，0），建立 与的递推关系 ，即 ，由数列  是等差数列，且 ，公差 可求得  （）， ． 用数学归纳法证明与自然数n有关的几何命题，由k过渡到k＋1常利用几何图形来分析图形前后演变情况． [例5] 有n个圆，其中每两个圆都相交于两点，并且每三个圆都不相交于同一点，求证：这n个圆把平面分成f(n)＝n2-n＋2个部分． 证明①当n＝1时，即一个圆把平面分成二个部分f(1)=2 又n＝1时，n2-n＋2＝2，∴命题成立 ②假设n＝k时，命题成立，即k个圆把平面分成f(k)＝k2-k＋2个 部分，那么设第k＋1个圆记⊙O，由题意，它与k个圆中每个圆 交于两点，又无三圆交于同一点，于是它与其它k个圆相交于2k 个点．把⊙O分成2k条弧而每条弧把原区域分成2块，因此这平 面的总区域增加2k块，即f(k＋1)＝k2-k＋2＋2k=(k＋1)2-(k＋1)＋2 即n＝k＋1时命题成立． 由①②可知对任何n∈N命题均成立． 说明: 本题如何应用归纳假设及已知条件，其关键是分析k增加“1”时，研究第k＋1个圆与其它k个圆的交点个数问题． [例6] 已知n≥2，n∈N 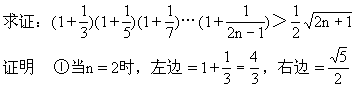 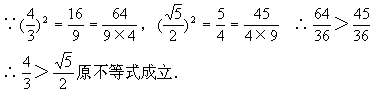 ②假设n=k时，原不等式成立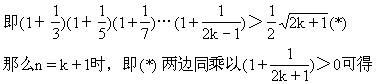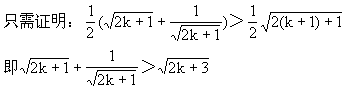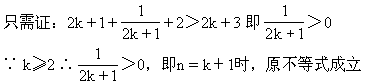．      由①②可知，对任何n∈N(n≥2)，原不等式均成立． 四、典型习题导练 1.用数学归纳法证明等式“1＋2＋3＋…＋（ ＋3）= ( N)”，当 =1时，左边应为____________.2.已知数列{ }的前n项和 ，则{}的前四项依次为_______,猜想=__________.3.已知数列   证明  .4.已知不等式  为大于2的整数， 表示不超过 的最大整数. 设数列 的各项为正，且满足 证明 .5. 自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能 力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，n∈N*，且x1＞0. 不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成正比，死亡量与xn2成正比， 这些比例系数依次为正常数a，b，c. （1）求xn+1与xn的关系式； （2）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量保持不变？ （3）设a＝2，c＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，则捕捞强度b的 最大允许值是多少？证明你的结论. (责任编辑：admin) |
- 上一篇：错解剖析得真知（七）
- 下一篇：错解剖析得真知（十三）