错解剖析得真知（七）
http://www.newdu.com 2025/05/19 11:05:46 人民教育出版社 佚名 参加讨论
错解剖析得真知（七） 第三章 基本初等函数Ⅱ（三角函数） 3.1任意角三角函数 一、知识导学 1．角：角可以看成由一条射线绕着端点从一个位置旋转到另一个位置所形成的几何图形.角的三要素是：顶点、始边、终边.角可以任意大小，按旋转的方向分类有正角、负角、零角. 2．弧度制：任一已知角  的弧度数的绝对值 ，其中 是以作为圆心角时所对圆弧的长， 为圆的半径.规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零.用“弧度”做单位来度量角的制度叫做弧度制.3．弧度与角度的换算：  ； ；1 .用弧度为单位表示角的大小时，弧度（rad）可以省略不写.度 不可省略.4．弧长公式、扇形面积公式：   ,其中 为弧长，为圆的半径.圆的周长、面积公式是弧长公式和扇形面积公式中当 时的情形.5．任意角的三角函数定义：设 是一个任意大小的角，角终边上任意一点P的坐标是 ，它与原点的距离是 ，那么角的正弦、余弦、正切、余切、正割、余割分别是 .这六个函数统称为三角函数.6．三角函数的定义域
7．三角函数值的符号：各三角函数值在第个象限的符号如图所示（各象限注明的函数为正，其余为负值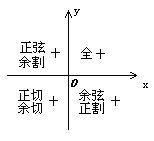）  可以简记为“一全、二正、三切、四余”为正. 二、疑难知识导析 1．在直角坐标系内讨论角 （1）角的顶点在原点，始边在  轴的正半轴上，角的终边在第几象限，就称这个角是第几象限角（或说这个角属于第几象限）.它的前提是“角的顶点为原点，角的始边为轴的非负半轴.否则不能如此判断某角为第几象限.若角的终边落在坐标轴上，就说这个角不属于任何象限.（2）与 角终边相同的角的集合表示. ，其中为任意角.终边相同的角不一定相等，相等的角终边一定相同，终边相同的角有无数多个，它们相差 整数倍.2．值得注意的几种范围角的表示法 “0  ～ 间的角”指 ；“第一象限角”可表示为 ；“小于90的角”可表示为 .3．在弧度的定义中  与所取圆的半径无关，仅与角的大小有关.4．确定三角函数的定义域时，主要应抓住分母为零时比值无意义这一关键.当终边在坐标轴上时点P坐标中必有一个为0. 5．根据三角函数的定义可知：（1）一个角的三角函数值只与这个角的终边位置有关，即角 与 的同名三角函数值相等；（2） ，故有 ，这是三角函数中最基本的一组不等关系.6．在计算或化简三角函数关系式时，常常需要对角的范围以及相应三角函数值的正负情况进行讨论.因此，在解答此类问题时要注意：（1）角的范围是什么？（2）对应角的三角函数值是正还是负？（3）与此相关的定义、性质或公式有哪些？ 三、经典例题导讲 [例1] 若A、B、C是  的三个内角，且 ，则下列结论中正确的个数是（ ）①.  ②. ③. ④. A．1 B.2 C.3 D.4 错解：  ∴ ，故选B错因：三角形中大角对大边定理不熟悉，对函数单调性理解不到位导致应用错误 正解：法1 在中，在大角对大边， 法2 考虑特殊情形，A为锐角，C为钝角，故排除B、C、D，所以选A . [例2]已知  角的终边关于 轴对称，则与 的关系为 .错解：∵ 角的终边关于轴对称，∴ + ，（ 错因：把关于 轴对称片认为关于轴的正半轴对称.正解：∵ 角的终边关于轴对称∴  即 说明：（1）若 角的终边关于 轴对称，则与的关系为 （2）若 角的终边关于原点轴对称，则与的关系为 （3）若 角的终边在同一条直线上，则与的关系为 [例3] 已知  ，试确定 的象限.错解：∵  ，∴ 是第二象限角，即 从而  故 是第三象限角或第四象限角或是终边在轴负半轴上的角.错因：导出 是第二象限角是正确的，由即可确定，而题中 不仅给出了符号，而且给出了具体的函数值，通过其值可进一步确定的大小，即可进一步缩小所在区间.正解：∵ ，∴是第二象限角，又由  知  ，故是第四象限角.[例4]已知角 的终边经过 ，求 的值.错解：   错因：在求得 的过程中误认为  0正解：若  ，则 ，且角在第二象限若  ，则 ，且角在第四象限 说明：（1）给出角的终边上一点的坐标，求角的某个三解函数值常用定义求解； （2）本题由于所给字母 的符号不确定，故要对的正负进行讨论.[例5] （1）已知 为第三象限角，则 是第 象限角， 是第 象限角；（2）若  ，则是第 象限角.解：（1）  是第三象限角，即  ， 当  为偶数时，为第二象限角当 为奇数时，为第四象限角而 的终边落在第一、二象限或轴的非负半轴上.（2）因为  ，所以为第二象限角.点评： 为第一、二象限角时，为第一、三象限角，为第三、四象限角时，为第二、四象限角，但是它们在以象限角平分线为界的不同区域.[例6]一扇形的周长为20  ，当扇形的圆心角等于多少时，这个扇形的面积最大？最大面积是多少？解：设扇形的半径为  ，则扇形的弧长 扇形的面积  所以当  时，即 时 .点评：涉及到最大（小）值问题时，通常先建立函数关系，再应用函数求最值的方法确定最值的条件及相应的最值. [例7]已知  是第三象限角，化简 .解：原式＝  ＝ 又 是第三象限角， 所以，原式＝  .点评：三角函数化简一般要求是：（1）尽可能不含分母；（2）尽可能不含根式；（3）尽可能 使三角函数名称最少；（4）尽可能求出三角函数式的值.本题的关健是如何应用基本关系式脱去根式，进行化简. [例8] 若角 满足条件 ，则在第（ ）象限A.一 B.二 C.三 D.四 解：  角在第二象限.故选B.[例9] 已知  ，且 .（1）试判断  的符号；（2）试判断  的符号.解：（1）由题意，  ，  ，所以 .（2）由题意知 为第二象限角， ，所以 .四、典型习题导练 1．已知钝角 的终边经过点 ，且 ，则的值为 ）A．  B． C． D． 2．角α的终边与角β的终边关于y轴对称，则β为（ ） A.-α B.л-α C.（2kл+1）л-α(k∈Z) D.kл-α（k∈Z） 3.若sinαtgα≥0,k∈Z，则角α的集合为（ ） A．[2k 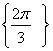 － ，2k +] B.( 2k－,2k+)C.( 2k －，2k+)∪ D.以上都不对4．当0＜x＜ 时,则方程cos (cosx)=0的解集为( )A.  B. C. D. 5．下列四个值:sin3,cos3,tg3,ctg3的大小关系是( ) A.cos3＜tg3＜ctg3＜sine B.sin3＞cos3＞tg3＞ctg3 C.cot3＜tan3＜cos3＜sin3 D.sin3＞tan3＞cos3＞cot3 6．已知x∈(0, ),则下面四式: 中正确命题的序号是 .①sinx＜x＜tgx ②sin(cosx)＜cosx＜cos(sinx) ③sin3x+cos3x＜1 ④cos(sinx)＜sin(cosx)＜cosx 7．有以下四组角：(1)k +；(2)k-；(3)2k±；(4)-k+(k∈z)其中终边相同的是（ ）A.(1)和(2) B.(1)、(2)和(3) C.(1)、(2)和(4) D.(1)、(2)、(3)和(4) 8．若角α的终边过点(sin30°，-cos30°),则sinα等于（ ） A. B.－ C.－ D.－ 9．函数y=  的定义域是______,值域是______.10．若点P  在第一象限，则在［０，2 ］内的取值范围是（ ）A.  B.  C.  D.  (责任编辑：admin) |
- 上一篇：错解剖析得真知（十五）
- 下一篇：错解剖析得真知（十四）