错解剖析得真知（十五）_高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

错解剖析得真知（十五）

http://www.newdu.com 2025/05/19 11:05:07 人民教育出版社佚名参加讨论

    错解剖析得真知（十五）
    第六章立体几何初步
    §6.1 两条直线之间的位置关系
    一、知识导学
    1.     平面的基本性质.公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内.公理2：如果两个平面有一个公共点，那么它们还有其他公共点，且所有这些公共点的集合是一条过这个公共点的直线.公理3：经过不在同一条直线上的三点，有且只有一个平面.推论1：经过一条直线和这条直线外的一点，，有且只有一个平面.推论2：经过两条相交直线，有且只有一个平面.推论3：经过两条平行直线，有且只有一个平面.
    2.     空间两条直线的位置关系，包括：相交、平行、异面.
    3.     公理4：平行于同一条直线的两条直线平行.定理4：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等.推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角（或直角）相等.
    4.     异面直线.异面直线所成的角；两条异面直线互相垂直的概念；异面直线的公垂线及距离.
    5.     反证法.会用反证法证明一些简单的问题.
    二、疑难知识导析
    1．异面直线是指不同在任何一个平面内，没有公共点.强调任何一个平面.
    2．异面直线所成的角是指经过空间任意一点作两条分别和异面的两条直线平行的直线所成的锐角（或直角）.一般通过平移后转化到三角形中求角，注意角的范围.
    3．异面直线的公垂线要求和两条异面直线垂直并且相交，
    4．异面直线的距离是指夹在两异面直线之间公垂线段的长度.求两条异面直线的距离关键是找到它们的公垂线.
    5．异面直线的证明一般用反证法、异面直线的判定方法：如图，如果b,A且A,a,则a与b异面.
    三、经典例题导讲
    [例1]在正方体ABCD-A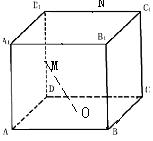BCD中,O是底面ABCD的中心，M、N分别是棱DD、DC的中点，则直线OM(     ).

    A .是AC和MN的公垂线.   B .垂直于AC但不垂直于MN.
    C .垂直于MN，但不垂直于AC. D .与AC、MN都不垂直.
    错解:B.
    错因：学生观察能力较差，找不出三垂线定理中的射影.
    正解：A.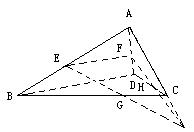

    [例2]如图，已知在空间四边形ABCD中,E,F分别是AB,AD的中点，G,H分别是BC,CD上的点,且,求证:直线EG,FH,AC相交于一点.
    错解：证明：、F分别是AB,AD的中点,
    ∥BD,EF=BD,
    又, GH∥BD,GH=BD,
         四边形EFGH是梯形，设两腰EG,FH相交于一点T,
     ,F分别是AD.AC与FH交于一点.
    直线EG,FH,AC相交于一点
    正解：证明：、F分别是AB,AD的中点,
       ∥BD,EF=BD,
    又,
         GH∥BD,GH=BD,
    四边形EFGH是梯形，设两腰EG,FH相交于一点T,
    平面ABC,FH平面ACD,
    T面ABC,且T面ACD,又平面ABC平面ACD=AC,
    ,直线EG,FH,AC相交于一点T.
    [例3]判断：若a,b是两条异面直线，P为空间任意一点，则过P点有且仅有一个平面与a,b都平行.
    错解：认为正确.
    错因：空间想像力不够.忽略P在其中一条线上，或a与P确定平面恰好与b平行，此时就不能过P作平面与a平行.
    正解：假命题．

    [例4] 如图，在四边形ABCD中，已知AB∥CD，直线AB，BC，AD，DC分别与平面α相交于点E，G，H，F．求证：E，F，G，H四点必定共线（在同一条直线上）．
      分析：先确定一个平面，然后证明相关直线在这个平面内，最后证明四点共线．
     证明 ∵ AB//CD， AB，CD确定一个平面β．
    又∵AB ∩α＝E，AB

β， Eα，Eβ，
     即 E为平面α与β的一个公共点．
    同理可证F，G，H均为平面α与β的公共点．
    ∵ 两个平面有公共点，它们有且只有一条通过公共点的公共直线，
    ∴ E，F，G，H四点必定共线．
    点评：在立体几何的问题中，证明若干点共线时，先证明这些点都是某两平面的公共点，而后得出这些点都在二平面的交线上的结论．
    [例5]如图，已知平面α，β，且α∩β＝．设梯形ABCD中，AD∥BC，且AB

α，CD

β，求证：AB，CD，共点（相交于一点）．
分析：AB，CD是梯形ABCD的两条腰，必定相交于一点M，只要证明M在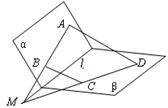上，而是两个平面α，β的交线，因此，只要证明M∈α，且M∈β即可．

    证明： ∵ 梯形ABCD中，AD∥BC，
    ∴AB，CD是梯形ABCD的两条腰．
    ∴ AB，CD必定相交于一点，
    设 AB ∩CD＝M．
    又∵ AB

α，CD

β，∴ M∈α，且M∈β．
    ∴ M∈α∩β．
    又∵ α∩β＝，∴ M∈，
    即 AB，CD，共点．
    点评：证明多条直线共点时，与证明多点共线是一样的．
     [例6]已知：a，b，c，d是不共点且两两相交的四条直线，求证：a，b，c，d共面．
     分析：弄清楚四条直线不共点且两两相交的含义：四条直线不共点，包括有三条直线共点的情况；两两相交是指任何两条直线都相交．在此基础上，根据平面的性质，确定一个平面，再证明所有的直线都在这个平面内．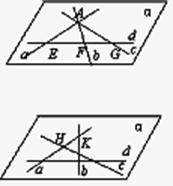

    证明 1?若当四条直线中有三条相交于一点，不妨设a，b，c相交于一点 A   ∴ 直线d和A确定一个平面α．
    又设直线d与a，b，c分别相交于E，F，G，
    则 A，E，F，G∈α．
    ∵ A，E∈α，A，E∈a，
    ∴ a

α．
同理可证 b

α，c

α．
    ∴ a，b，c，d在同一平面α内．
    2?当四条直线中任何三条都不共点时，如图．
    ∵ 这四条直线两两相交，
    则设相交直线a，b确定一个平面α．
    设直线c与a，b分别交于点H，K，
    则 H，K∈α．
    又∵ H，K∈c，∴ c

α．
同理可证 d

α．
    ∴ a，b，c，d四条直线在同一平面α内．
    点评：证明若干条线(或若干个点)共面的一般步骤是：首先由题给条件中的部分线(或点)确定一个平面，然后再证明其余的线(或点)均在这个平面内．本题最容易忽视“三线共点”这一种情况．因此，在分析题意时，应仔细推敲问题中每一句话的含义．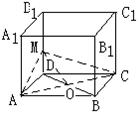

    [例7] 在立方体ABCD－A₁B₁C₁D₁中，
    （1）找出平面AC的斜线BD₁在平面AC内的射影；
    （2）直线BD₁和直线AC的位置关系如何？
    （3）直线BD₁和直线AC所成的角是多少度？
    解：(1)连结BD, 交AC于点O .
    (2)BD₁和AC是异面直线.
    (3)过O作BD₁的平行线交DD₁于点M，连结MA、MC，则∠MOA或其补角即为异面直线AC和BD₁所成的角.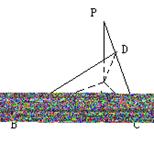

    不难得到MA＝MC，而O为AC的中点，因此MO⊥AC，即∠MOA＝90°，
    ∴异面直线BD₁与AC所成的角为90°.
    [例8] 已知：在直角三角形ABC中，A为直角，PA⊥平面ABC，BD⊥PC，垂足为D，求证：AD⊥PC
    证明：∵　PA ⊥平面ABC∴　PA⊥BA
    又∵　BA⊥AC ∴　BA⊥平面PAC
    ∴　AD是BD在平面PAC内的射影
    又∵　BD⊥PC ∴　AD⊥PC.（三垂线定理的逆定理）
    四、典型习题导练
    1．如图, P是△ABC所在平面外一点，连结PA、PB、PC后，在包括AB、BC、CA的六条棱所在的直线中，异面直线的对数为( )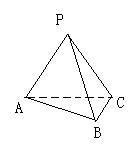

     A.2对   B.3对   C.4对 D.6对
    2. 两个正方形ABCD、ABEF所在的平面互相垂直，则异面直线AC和BF所成角的大小为    　．
    3. 在棱长为a的正方体ABCD－A₁B₁C₁D₁中，体对角线DB₁与面对角线BC₁所成的角是      ，它们的距离是     .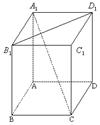

    4.长方体中，
    则所成角的大小为_ ___.
    5.关于直角AOB在定平面α内的射影有如下判断：①可能是0°的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180°的角. 其中正确判断的序号是_____.（注：把你认为正确的序号都填上）.

    6．在空间四边形ABCD中，AB⊥CD，AH⊥平面BCD，
    求证：BH⊥CD
    7．如图正四面体中，D、E是棱PC上不重合的两点；F、H分别是棱PA、PB上的点，且与P点不重合．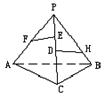

求证：EF和DH是异面直线．
(责任编辑：admin)

错解剖析得真知（十五）

http://www.newdu.com 2025/05/19 11:05:07 人民教育出版社 佚名 参加讨论

http://www.newdu.com 2025/05/19 11:05:07 人民教育出版社佚名参加讨论