错解剖析得真知（十六）
http://www.newdu.com 2025/05/19 02:05:36 人民教育出版社 佚名 参加讨论
错解剖析得真知（十六） §6.2直线与平面之间的位置关系 一、知识导学 1. 掌握空间直线与平面的三种位置关系（直线在平面内、相交、平行）. 2. 直线和平面所成的角，当直线与平面平行或在平面内时所成的角是  ，当直线与平面垂直时所成的角是9，当直线与平面斜交时所成的角是直线与它在平面内的射影所成的锐角.3. 掌握直线与平面平行判定定理（如果平面外的一条直线和平面内的一条直线平行，那么这条直线和平面平行）和性质定理（如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行）. 4. 直线与平面垂直的定义是：如果一条直线和一个平面内所有直线垂直，那么这条直线和这个平面垂直；掌握直线与平面垂直的判定定理（如果一条直线和平面内的两条相交直线都垂直，那么这条直线垂直于这个平面）和性质定理（如果两条直线同垂直于一个平面，那么这两条直线平行）. 5. 直线与平面的距离（一条直线和一个平面平行时，这条直线上任意一点到这个平面的距离，叫做这条直线和这个平面的距离）. 6. 三垂线定理（在平面内的一条直线，如果和这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直）、逆定理（在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线在这个平面内的射影垂直）. 7. 从平面外一点向这个平面所引的垂线段和斜线段中：①射影相等的两条斜线段相等，射影较长的斜线段也较长；②相等的斜线段的射影相等，较长的斜线段的射影也较长；③垂线段比任何一条斜线段都短. 二、疑难知识导析 1.斜线与平面所成的角关键在于找射影，斜线与平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角. 2.在证明平行时注意线线平行、线面平行及面面平行判定定理和性质定理的反复运用. 3.在证明垂直时注意线线垂直、线面垂直及面面垂直判定定理和性质定理的反复运用，同时还要注意三垂线定理及其逆定理的运用.要注意线面垂直的判定定理中的“两条相交直线”，如果用“无数”或“两条”都是错误的. 4.直线与平面的距离一般是利用直线上某一点到平面的距离.“如果在平面的同一侧有两点到平面的距离（大于0）相等，则经过这两点的直线与这个平面平行.”要注意“同一侧”、“距离相等”. 三、经典例题导讲 [例1]已知平面  ∥平面 ，直线  平面,点P 直线,平面、间的距离为8，则在内到点P的距离为10，且到的距离为9的点的轨迹是（ ）A.一个圆 B.四个点 C.两条直线 D .两个点 错解：A. 错因：学生对点线距离、线线距离、面面距离的关系掌握不牢. 正解：B. [例2] a和b为异面直线，则过a与b垂直的平面( ). A．有且只有一个 B．一个面或无数个 C．可能不存在 D．可能有无数个 错解：A. 错因：过a与b垂直的平面条件不清. 正解：C. [例3]由平面 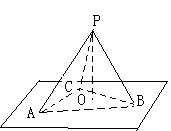外一点P引平面的三条相等的斜线段，斜足分别为A,B,C，O为⊿ABC的外心，求证： . 错解：因为O为⊿ABC的外心，所以OA＝OB＝OC，又因为PA＝PB＝PC，PO公用，所以⊿POA，⊿POB，⊿POC都全等，所以  POA＝POB＝POC＝ ，所以 .错因：上述解法中 POA＝POB＝POC＝RT，是对的，但它们为什么是直角呢？这里缺少必要的证明.正解：取BC的中点D，连PD、OD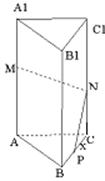，   [例4]如图，在正三棱柱ABC-A1B1C1中，AB=3，AA1=4,M为AA1的中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M点的最短路线长为  ，设这条最短路线与C1C的交点为N,求: （1）该三棱柱的侧面展开图的对角线长； （2）PC和NC的长； （3）平面NMP和平面ABC所成二面角（锐角）的大小（用反三角函数表示） 错因：（1）不知道利用侧面BCC1 B1展开图求解,不会找 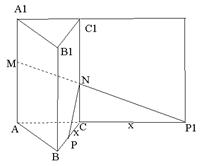的线段在哪里;(2)不会找二面角的平面角. 正解：(1)正三棱柱ABC-A1B1C1的侧面展开图是一个长为9，宽为4的矩形，其对角线长为  (2)如图，将侧面BC1旋转  使其与侧面AC1在同一平面上，点P运动到点P1的位置，连接MP1 ，则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线.设PC＝  ，则P1C＝ ，在   (3)连接PP1（如图），则PP1就是平面NMP与平面ABC的交线，作NH  于H，又CC1 平面ABC，连结CH，由三垂线定理的逆定理得， .    [例5] P是平行四边形ABCD 所在平面外一点，Q 是PA 的中点，求证：PC∥ 平面BDQ ． 分析：要证明平面外的一条直线和该平面平行，只要在该平面内找到一条直线和已知直线平行就可以了． 证明：如图所示，连结AC ，交BD 于点O 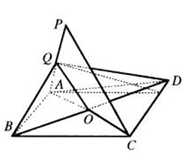，  ∵四边形ABCD 是平行四边形. ∴AO=CO ，连结OQ ，则OQ 在平面BDQ 内，且OQ 是  的中位线，∴PC∥OQ ． ∵PC 在平面BDQ 外，∴PC∥平面BDQ ． 点 评：应用线面平行的判定定理证明线面平行时，关键是在平面内找一条直线与已知直线平行. [例6] 在正方体A1B1C1D1－ABCD中，E、F分别是棱AB、BC的中点，O是底面ABCD的中点．求证：EF垂直平面BB1O．  证明 ： 如图,连接AC、BD，则O为AC和BD的交点． ∵E、F分别是AB、BC的中点， ∴EF是△ABC的中位线，∴EF∥AC． ∵B1B⊥平面ABCD,AC 平面ABCD∴AC⊥B1B，由正方形ABCD知：AC⊥BO， 又BO与BB1是平面BB1O上的两条相交直线， ∴AC⊥平面BB1O(线面垂直判定定理) ∵AC∥EF， ∴ EF⊥平面BB1O． [例7]如图，在正方体ABCD-A1B1C1D1 中，E 是BB1 的中点，O 是底面正方形ABCD 的中心，求证：OE 平面ACD1 ．分析：本题考查的是线面垂直的判定方法．根据线面垂直的判定方法，要证明OE 平面ACD1 ，只要在平面ACD1 内找两条相交直线与OE 垂直．证明：连结B1D 、A!D 、BD ，在△B1BD 中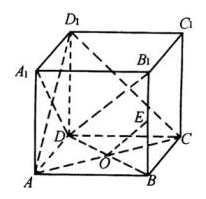，  ∵E,O 分别是B1B 和DB 的中点， ∴EO∥B1D ． ∵B1A1 面AA1D1D ，∴DA1 为DB1 在面AA1D1D 内的射影． 又∵AD1 A1D ，∴AD1 DB1 ．同理可证B1D D1C ．又∵AD1  ，AD1,D1C 面ACD1 ，∴B1D 平面ACD1 ．∵B1D∥OE ， ∴OE 平面ACD1 ．点 评：要证线面垂直可找线线垂直，这是立体几何证明线面垂直时常用的转化方法．在证明线线垂直时既要注意三垂线定理及其逆定理的应用，也要注意有时是从数量关系方面找垂直，即勾股定理或余弦定理的应用． [例8]．如图，正方体ABCD-A1B1C1D1中,点N在BD上, 点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B. 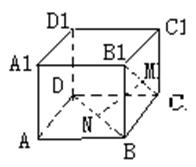 证明： 证法一.如图,作ME∥BC,交BB1于E,作NF∥AD,交AB于F,连EF则EF 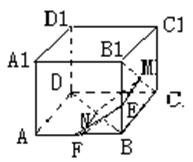平面AA1B1B.       ME=NF又ME∥BC∥AD∥NF, MEFN为平行四边形,MN∥EF. MN∥平面AA1B1B.证法二.如图,连接并延长CN交BA延长线于点P,连B1P,则B1P 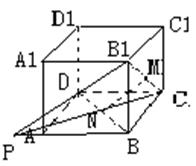平面AA1B1B.  ∽ , 又CM=DN,B1C=BD,   ∥B1P. B1P平面AA1B1B, MN∥平面AA1B1B.证法三.如图,作MP∥BB1,交BC于点P,连NP.  MP∥BB1, BD=B1C,DN=CM,  NP∥CD∥AB.面MNP∥面AA1B1B.MN∥平面AA1B1B.四、典型习题导练 1．设a ，b 是空间两条垂直的直线，且b∥平面 ．则在“a∥平面 ”、“a ”、“a与相交”这三种情况中，能够出现的情况有（ ）．A．0个 B．1 C．2个 D．3个 2．一个面截空间四边形的四边得到四个交点，如果该空间四边形仅有一条对角线与这个截面平行，那么此四个交点围成的四边形是（ ）． A．梯形 B．任意四边形 C．平行四边形 D．菱形 3．若一直线和一个平面平行，夹在直线和平面间的两条线段相等，那么这两条线段的位置关系是（ ）． A．平行 B．相交 C．异面 D．平行、相交或异面 4．空间四边形的边AB 、BC 、CD 、DA 的中点分别是E 、F 、G 、H ，若两条对角线BD 、AC 的长分别为2和4，则EG2+HF2 的值（ ）． A．5 B．10 C．20 D．40 5．点P 、Q 、R 、S 分别是空间四边形ABCD 四边的中点，则：当AC  时，四边形PQRS 是______形；当AC=BD 时，四边形PQRS 是____形．6．已知两个全等的矩形ABCD 和ABEF 不在同一平面内，M 、N 分别在它们的对角线AC ，BF 上，且CM=BN 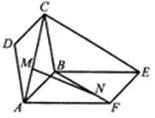，  求证：MN∥ 平面BCE ． 8. 如图，已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且   (1) 证明C1C ;当  的值为多少时，能使A1C平面C1BD？请给出证明.(责任编辑：admin) |
- 上一篇：对一道函数与方程调研题的思考
- 下一篇：错解剖析得真知（十五）