对一道函数与方程调研题的思考
http://www.newdu.com 2025/06/10 05:06:21 人民教育出版社 佚名 参加讨论
对一道函数与方程调研题的思考 江苏省徐州一中 张培强 题目（2011届徐州市高三第三次质检）若关于 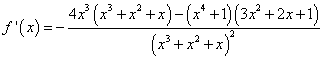 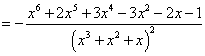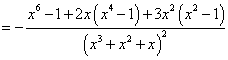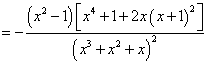的方程 有实数根，则实数 的取值范围为  ．解析1：⑴若  ，方程即为 ，可知方程无实根；⑵若  ，则方程可化为 ，设 ，    ，令  ，解得 或 ，列表如下：
计算得  ， ．故 的取值范围为 ．注析：方程的形式极易让我们将参数 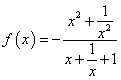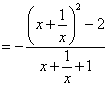分离出来，但随之产生的分式函数让人望而却步．关键在 中的分子上，将对应系数相同的项合并，可提取出公因式 ．事实上，对于高次问题，我们可以想方设法去降次，让题目变得和蔼一些．解析2：考虑 ，上下同时除以 ，可得  ，令 （ 或 ），则  ，由函数 的单调性易得， ，故的取值范围为．注析：同样是考虑方程的形式，各项系数呈现左右对称的关系．考虑方程，除以 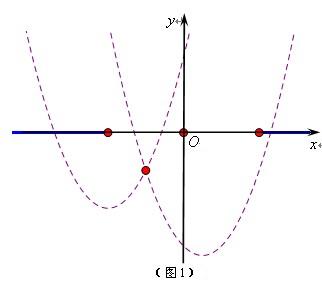后得到美妙的形式： ，即 ，换元后可考虑一元二次方程的根解决问题．解析3：令  （ 或 ），则问题转化为关于 的方程 在 内有实数根． ，令 ，则 ，所以方程有实根必须 或 （示意图如图1），即 或 ，解得 或 ，故 ． 注析：与解析2比较，考虑一元二次方程在定区间内的根的分布需要分类讨论，而试题的特殊性在于 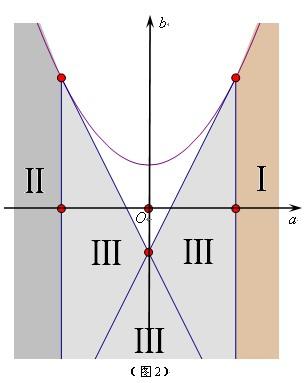 ，因此也省去了多种情况的讨论．变式 已知关于 的方程 有实数根（、 为实数），则 的最小值为 ．解析：⑴若 ，方程即为，可知方程无实根；⑵若 ，方程两边同除以，可得 ，即 ，令（或），则问题转化为关于的方程 在内有实数根．当  ，即 时，只需 ，可行域如图（2—Ⅰ），此时， ；当  ，即 时，只需，可行域如图（2—Ⅱ），此时，；当  ，即 时，只需 或 ，即 或 ，可行域如图（2—Ⅲ），此时 ． 综上可知， 的最小值为 ．注析：由于方程中含有两个参数，分离方法已不好使，而考虑换元后的方程的根，需要分类讨论解决．事实上，本题也可直接用求根公式求出方程的根，通过建立不等式得到关于 、的约束条件．面对一个形式复杂的问题，关键是将其转化，使之以和蔼可亲的面目呈现．如此，方可思路顺畅、下笔从容．诚然，问题的顺利解决需要我们扎实的知识功底和从容应变的能力． (责任编辑：admin) |
- 上一篇：错解剖析得真知（八）
- 下一篇：错解剖析得真知（十六）