错解剖析得真知(八)
http://www.newdu.com 2025/05/20 12:05:29 人民教育出版社 佚名 参加讨论
错解剖析得真知(八) 3.2三角函数基本关系式与诱导公式 一、知识导学 1.同角三角函数的基本关系式 平方关系: 同角三角函数的基本关系式可用图表示 (1)三个阴影部分三角形上底边平方和等于1的平方; (2)对角为倒数关系; (3)每个三角函数为相邻两函数的积. 2.诱导公式(
诱导公式可将“负角正化,大角小化,钝角锐化”. 3.诱导公式解决常见题型 (1)求值:已知一个角的某个三角函数,求这个角其他三角函数; (2)化简:要求是能求值则求值,次数、种类尽量少,尽量化去根式,尽可能不含分母. 二、疑难知识导析 1.三角变换的常见技巧 “1”的代换; 2.在进行三角函数化简和三角等式证明时,细心观察题目的特征,灵活恰当地选用公式,一般思路是将切割化弦.尽量化同名,同次,同角; 3.已知角 三、典型例题导讲 [例1]已知 错解:两边同时平方,由 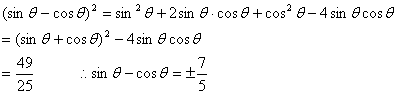 ∴ 或 错因:没有注意到条件 所以 正解: 两边同时平方,有 求出 [例2]若sinA=asinB,cosA=bcosB,A、B为锐角且a>1,0<b<1,求tanA的值 错解:由 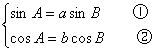 得tan A= 得tan A=错因:对题目最终要求理解错误.不清楚最后结论用什么代数式表示 正解:由 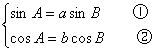 ①2+②2得a2sin2B+b2cos2B=1 ①2+②2得a2sin2B+b2cos2B=1∴cos2B= ∵B为锐角 ∴tan B= [例3](05年高考重庆卷)若函数 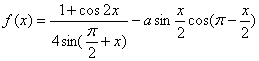 的最大值为2,试确定常数a的值. 的最大值为2,试确定常数a的值.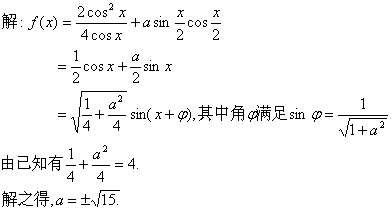 点评:本试题将三角函数“ [例4] (05年高考北京卷)已知 (1) 解:(1)∵ tan  ; ;所以 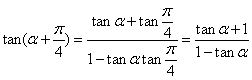 = = ; ;(2)由(I), tanα=- 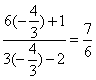 . .点评:本题设计简洁明了,入手容易,但对两角和与差的三角函数、同角间的基本关系式要求熟练应用,运算准确. [例5]化简: 错解:原式 错因:对三角函数诱导公式不完全理解,不加讨论而导致错误. 正解:原式 (1)当 原式 (2)当 原式 [例6](05年高考江苏卷)若 A. 错解: 错因:诱导公式应用符号错. 正解: =— [例7].(05年高考福建卷)已知 (1)求sinx-cosx的值; (2)求 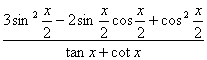 的值. 的值.解法一:(1)由 即 又 (2) 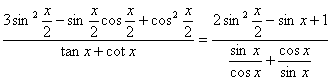 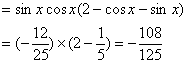
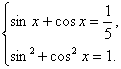 由①得 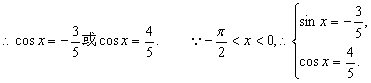 故 故 (2) 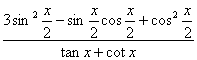 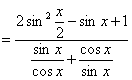 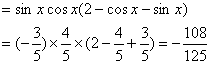 点评:本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力. [例8] (1)化简: + (2)设sin(α+)=-,且sin2α>0 求sinα,tanα 解:原式=+ +cos2αcsc2α =cos2α+sin2α+cos2αcsc2α =1+cot2α =csc2α (2)解:由sin(α+ )=- ∴cosα=- ∵sin2α>0∴2kπ<2α<2kπ+π kπ<α<kπ+ (k∈z) ∴α为第一象限或第二象限的角 ∵cosα=- <0 ∴α为第三角限角 sinα=-= tan α= = 点评:本题要求同学们熟练掌握同角三角函数之间的关系,在求值过程中特别注意三角函数值的符号的探讨. [例9] 求函数 解:由题意有 当 当 当 点评:有部分同学可能会认为不等式组(*)两者没有公共部分,所以定义域为空集,原因是没有正确理解弧度与实数的关系,总认为二者格格不入,事实上弧度也是实数. [例10] (05年高考天津卷) 已知 解法一:由题设条件,应用两角差的正弦公式得 即 由题设条件,应用二倍角余弦公式得 由①式和②式得 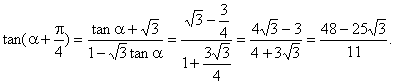 解法二:由题设条件,应用二倍角余弦公式得 由 由于 故 从而 点评: 四、典型习题导练 1. 当0<x<л时,则方程cos (лcosx)=0的解集为( ) A. 2.(05年高考全国卷Ⅰ)在 ① ③ 其中正确的是 A.①③ B.②④ C.①④ D.②③ 3.(05年全国卷Ⅲ)设 A. 4.函数 A. 增函数 B. 减函数 C. 偶函数 D. 奇函数 5.曲线 次记为P1,P2,P3,…,则|P2P4|等于( ) A. 6. 7.已知函数f(x)=2sinxcosx+cos2x. (1) 求f( 8.(05年高考湖南卷)已知在△ABC中,sinA(sinB+cosB)-sinC=0, sinB+cos2C=0,求角A、B、C的大小. 9.(06年高考安徽卷)已知 (1)求 (2)求 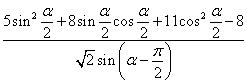 的值. 的值.(责任编辑:admin) |
- 上一篇:错解剖析得真知(十七)
- 下一篇:对一道函数与方程调研题的思考