错解剖析得真知(十)
http://www.newdu.com 2025/05/19 10:05:10 人民教育出版社 佚名 参加讨论
错解剖析得真知(十) 3.4三角函数的图象与性质 一、知识导学 1.三角函数线.设角 2.三角函数的图象 (1) (2)函数 ①“五点作图法” ②图象变化规律 3.三角函数的定义域、值域及周期 4.三角函数的奇偶性和单调性 二、疑难知识导析 1. 如: 2.用“五点法”作 3. 4.三角函数的定义域是研究其它一切性质的前提.求定义域实质上是解简单的三角不等式(组).要考虑到分母不为零,偶次根式被开方数不小于零,对数的真数大于零、底数大于零且不等于1,同时还要考虑到函数本身的定义域.可用三角函数图象或三角函数线解不等式(组). 5.求三角函数的值域是常见题型.一类是 6. 7.利用单调性比较函数值的大小.往往先利用对称型或周期性转化成同一单调区间上的两个同名函数. 三、典型例题导讲 [例1] 为了得到函数 A 向右平移 错解:A 错因:审题不仔细,把目标函数搞错是此题最容易犯的错误. 正解:B [例2] 函数 A 错解:A 错因:将函数解析式化为 正解:B [例3]下列四个函数y=tan2x,y=cos2x,y=sin4x,y=cot(x+ A.1 B.2 C.3 D.4 错解:B 错因:对三角函数图象的对称性和平移变换未能熟练掌握. 正解:D [例4]函数 A. 错解:B 错因:不注意内函数的单调性. 正解: C [例5]函数 解: [例6] 函数 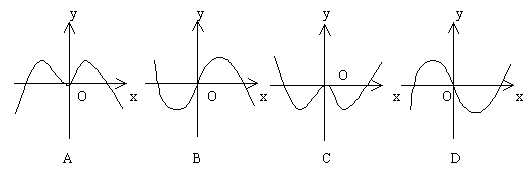 解:选D. 提示:显然 [例7] 当 A. 最大值为1,最小值为-1 B. 最大值为1,最小值为 C. 最大值为2,最小值为 解:选D 解析: [例8]已知定义在区间 其图象如图所示. 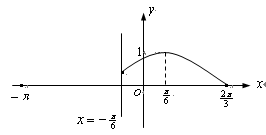 (1)求函数 (2)求方程 解:(1)当 由函数 函数 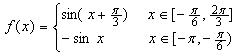 . .(2)当 当 ∴方程 四、典型习题导练 1.函数 A. C. 2.已知点 试根据图象特征判定下列四个不等式的正确性:① 3. 4.若常数α满足 5.已知函数 (1)当y取最大值时,求自变量x的集合; (2)该函数的图象可由y=sinx, 6. 求函数的最小值. 7.(06年高考浙江卷)如图,函数y=2sin(πx+φ),x∈R,(其中0≤φ≤ 的图象与y轴交于点(0,1). (1)求φ的值; (2)设P是图象上的最高点,M、N是图象与x轴的交点,求 3.5解三角形及三角函数的应用 一、知识导学 1.解三角形的的常用定理: (1) 内角和定理: (2) 正弦定理: (3) 余弦定理: (4) 勾股定理: 2.解三角形是指已知三角形中的部分元素运用边角的关系求得其他的边角的问题. 三角函数的应用是指用三角函数的理论解答生产、科研和日常生活中的实际应用问题.他的显著特点是(1)意义反映在三角形的边、角关系上,有直角三角形,也有斜三角形.(2)函数模型多种多样,有三角函数,有代数函数,有时一个问题中三角函数与代数函数并存.解三角函数应用题一般首先审题,三角函数应用题多以“文字语言,图形语言”并用的方式,要通过审题领会其中的数的本质,将问题中的边角关系与三角形联系起来,确定以什么样的三角形为模型,需要哪些定理或边角关系列出等量或不等量关系的解题思路;其次,寻求变量之间的关系,也即抽象出数学问题,要充分运用数形结合的思想、图形语言和符号语言等方式来思考解决问题;再次,讨论对数学模型的性质对照讨论变量的性质,从而得到的是数学参数值;最后,按题目要求作出相应的部分问题的结论. 二、疑难知识导析 1.对各类定理的应用要注意使用其变形逆用.同时充分利用方程的思想知道其中的部分量可求出其他量. 2.三角函数的应用主要是图象和性质的应用. 3.三角形中元素关系的应用与实际问题中的应用关键是如何建立数模结构. 三、经典例题导讲 [例1]已知方程 且 错解: 由 错因:忽略了隐含限制 正解: 又 由 答案: -2 . [例2]在 ①若 ②若 ③ ④若 ⑤若 错解:③④⑤中未考虑 错因:④中未检验. 正解:错误命题③⑤. ① ② ③ 显然 ④ 或 ⑤ [例3]函数f(x)= 错解: 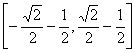 错因:令 正解:  [例4] (06年高考江苏卷) 【思路点拨】本题考查三角公式的记忆及熟练运用三角公式计算求值 解: = =  【解后反思】方法不拘泥,要注意灵活运用,在求三角的问题中,要注意这样的口决“三看”即(1)看角,把角尽量向特殊角或可计算角转化,(2)看名称,把一道等式尽量化成同一名称或相近的名称,例如把所有的切都转化为相应的弦,或把所有的弦转化为相应的切,(3)看式子,看式子是否满足三角函数的公式.如果满足直接使用,如果不满足转化一下角或转换一下名称,就可以使用. [例5] 在锐角△ABC中,A<B<C,且B=60°, 解:∵B=60° ∴A+C=120° cos(A+C)=- 又由已知 ∴cosAcosC= ∴cos(C-A)= ∴A=45° B=60° C=75° ∴a+ [例6]如图,在平面有点A、B、P、Q,其中 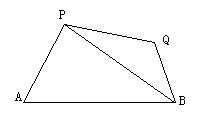 解:设∠BAP=α α∈[0, ∠BQP=β,在△PAB,△PBQ中 由余弦定理cosβ=cosα-1 ∴S2+T2=( =- ∴当cosα=1时,S2+T2有最小值 当cosα= [例7]已知函数f(x)=sin(wx+j),x?R,(其中w>0)的图象与x轴在原点右侧的第一个交点为N(6,0),又f(2+x)=f(2-x),f(0)<0,求这个函数的解析式. 解: 将N(6,0)代入f(x)=sin( 得:j=2k [例8] 已知△ABC的周长为6, (1)△ABC的面积S的最大值; (2) 解 设 由余弦定理得 故有 (1)所以 (2)所以 四、典型习题导练 1.在Rt△ABC中,C=90°,则sinAcos2(45°- A.有最大值 C.即无最大值也无最小值 D.有最大值 2.要得到y=sin2x的图象,只需将y=cos(2x- A.向右平移 3.电流强度I(安)随时间t(秒)变化的函数 I= 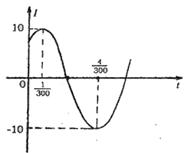 4.在△ABC中,sin 5.直角三角形的周长为定值2l,则斜边的最小值是 . 6.如果方程x2-4xcosθ+2=0与方程2x2+4xsin2θ-1=0有一根,互为倒数求θ值, 其中0<θ<π. 7.已知一半径为1,圆心角为 8.在 (责任编辑:admin) |
- 上一篇:错解剖析得真知(十一)
- 下一篇:错解剖析得真知(十八)