错解剖析得真知(十一)
http://www.newdu.com 2025/05/19 06:05:24 人民教育出版社 佚名 参加讨论
错解剖析得真知(十一) 第四章 数列 §4.1等差数列的通项与求和 一、知识导学 1.数列:按一定次序排成的一列数叫做数列. 2.项:数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项(或首项),第2项,…,第n项,…. 3.通项公式:一般地,如果数列{an}的第n项与序号n之间的关系可以用一个公式来表示,那么这个公式叫做这个数列的通项公式. 4. 有穷数列:项数有限的数列叫做有穷数列. 5. 无穷数列:项数无限的数列叫做无穷数列 6.数列的递推公式:如果已知数列的第一项(或前几项)及相邻两项(或几项)间关系可以用一个公式来表示,则这个公式就叫做这个数列的递推公式.递推公式是给出数列的一种重要方法,其关健是先求出a1,a2,然后用递推关系逐一写出数列中的项. 7.等差数列:一般地,如果一个数列从第二项起,每一项减去它的前一项所得的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示. 8.等差中项:如果a,A,b这三个数成等差数列,那么A= 二、疑难知识导析 1.数列的概念应注意几点:(1)数列中的数是按一定的次序排列的,如果组成的数相同而排列次序不同,则就是不同的数列;(2)同一数列中可以出现多个相同的数;(3)数列看做一个定义域为正整数集或其有限子集({1,2,3,…,n})的函数. 2.一个数列的通项公式通常不是唯一的. 3.数列{an}的前n项的和Sn与an之间的关系: 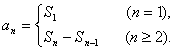 若a1适合an(n>2),则 若a1适合an(n>2),则4.从函数的角度考查等差数列的通项公式:an= a1+(n-1)d=d·n+ a1-d, an是关于n的一次式;从图像上看,表示等差数列的各点(n, 5、对等差数列的前n项之和公式的理解:等差数列的前n项之和公式可变形为 6、在解决等差数列问题时,如已知,a1,an,d, 三、经典例题导讲 [例1]已知数列1,4,7,10,…,3n+7,其中后一项比前一项大3.(1)指出这个数列的通项公式;(2)指出1+4+…+(3n-5)是该数列的前几项之和. 错解:(1)an=3n+7; (2) 1+4+…+(3n-5)是该数列的前n项之和. 错因:误把最后一项(含n的代数式)看成了数列的通项.(1)若令n=1,a1=10 正解:(1)an=3n-2; (2) 1+4+…+(3n-5)是该数列的前n-1项的和. [例2] 已知数列 求数列 错解: ① ② 错因:在对数列概念的理解上,仅注意了an=Sn-Sn-1与的关系,没注意a1=S1. 正解: ①当 当 经检验 ②当 当 ∴ [例3] 已知等差数列 错解:S30= S10·2d. 错因:将等差数列中Sm, S2m -Sm, S3m -S2m成等差数列误解为Sm, S2m, S3m成等差数列. 正解:由题意: 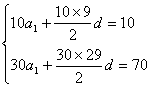 得 得代入得S40 = [例4]等差数列 错解:因为等差数列的通项公式是关于n的一次函数,故由题意令an=7n+1;bn=4n+27. 错因:误认为 正解: [例5]已知一个等差数列 错解:由an 当n 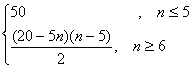 错因:一、把n 正解: 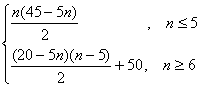 [例6]已知一个等差数列的前10项的和是310,前20项的和是1220, 由此可以确定求其前 解:理由如下:由题设: 得: 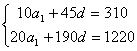 ∴ [例7]已知: 解:(1) 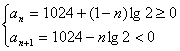 (2) 当 令: 得: ∵ [例8]项数是 证明:依题意 ∵ ∵ ∴ 四、典型习题导练 1.已知 2.设 3.求和: 4.求和: 5.已知 6.在等差数列 A.72 B.60 C.48 D.36 7. 已知 8.已知数列 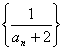 成等差数列,且 成等差数列,且§4.2等比数列的通项与求和 一、知识导学 1. 等比数列:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于 同 一个 常 数,那 么 这 个 数 列 就 叫 做 等 比 数 列,这个常数叫做等比数列的公比,公比通常用字母q表示. 2. 等比中项:若a,G,b成等比数列,则称G 为a 和b 的等比中项. 3.等比数列的前n项和公式: 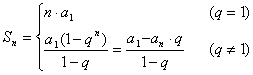 二、疑难知识导析 1.由于等比数列的每一项都可能作分母,故每一项均不为0,因此q也不为0. 2.对于公比q,要注意它是每一项与它前一项的比,防止把相邻两项的比的次序颠倒. 3.“从第2项起”是因为首项没有“前一项”,同时应注意如果一个数列不是从第2项起,而是从第3项或第4项起每一项与它前一项的比都是同一个常数,此数列不是等比数列,这时可以说此数列从. 第2项或第3项起是一个等比数列. 4.在已知等比数列的a1和q的前提下,利用通项公式an=a1qn-1,可求出等比数列中的任一项. 5.在已知等比数列中任意两项的前提下,使用an=amqn-m可求等比数列中任意一项. 6.等比数列{an}的通项公式an=a1qn-1可改写为 7.在解决等比数列问题时,如已知,a1,an,d, 三、经典例题导讲 [例1] 已知数列 A.等差数列 B.等比数列 C.既不是等差数列,也不是等比数列 D.既是等差数列,又是等比数列 错解: 错因:忽略了 正解:当n=1时,a1=S1=aq; 当n>1时, 但 [例2] 已知等比数列 错解:S30= S10·q 2. 错因:是将等比数列中Sm, S2m -Sm, S3m -S2m成等比数列误解为Sm, S2m, S3m成等比数列. 正解:由题意: 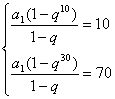 得 得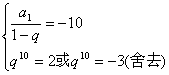 , ,[例3] 求和:a+a2+a3+…+an. 错解: 错因:是(1)数列{an}不一定是等比数列,不能直接套用等比数列前n项和公式(2)用等比数列前n项和公式应讨论q是否等于1. 正解:当a=0时,a+a2+a3+…+an=0; 当a=1时,a+a2+a3+…+an=n; 当a [例4]设 求证: 证明: 证法一:关于 ∴ 则必有: 设公比为 ∵ 证法二:∵ ∴ ∴ ∵ [例5]在等比数列 解: ∵ [例6]求数列 解: 两式相减: 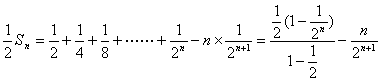 [例7]从盛有质量分数为20%的盐水2kg的容器中倒出1kg盐水,然后加入1kg水,以后每次都倒出1kg盐水,然后再加入1kg水, 问:(1)第5次倒出的的1kg盐水中含盐多kg? (2)经6次倒出后,一共倒出多少kg盐?此时加1kg水后容器内盐水的盐的质量分数为多少? 解:(1)每次倒出的盐的质量所成的数列为{an},则: a1= 0.2 (kg), a2= 由此可见:an= ( (2)由(1)得{an}是等比数列 a1=0.2 , q= 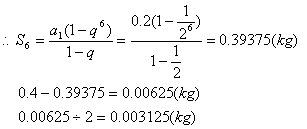 答:第5次倒出的的1kg盐水中含盐0.0125kg;6次倒出后,一共倒出0.39375kg盐,此时加1kg水后容器内盐水的盐的质量分数为0.003125。 四、典型习题导练 1.求下列各等比数列的通项公式: 1) a1=-2, a3=-8 2) a1=5, 且2an+1=-3an 3) a1=5, 且 2.在等比数列 3.已知无穷数列 求证:(1)这个数列成等比数列 (2)这个数列中的任一项是它后面第五项的 (3)这个数列的任意两项的积仍在这个数列中。 4.设数列 5.已知数列{an}中,a1=-2且an+1=Sn,求an ,Sn 6.是否存在数列{an},其前项和Sn组成的数列{Sn}也是等比数列,且公比相同? 7.在等比数列 (责任编辑:admin) |
- 上一篇:错解剖析得真知(十九)
- 下一篇:错解剖析得真知(十)