错解剖析得真知(二十)
http://www.newdu.com 2025/05/19 02:05:29 人民教育出版社 佚名 参加讨论
错解剖析得真知(二十) 第七章 平面解析几何初步 §7.1直线和圆的方程 一、知识导学 1.两点间的距离公式:不论A( 2.定比分点公式:定比分点公式是解决共线三点A( 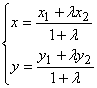 .当P点为AB的中点时,λ=1,此时中点坐标公式是 .当P点为AB的中点时,λ=1,此时中点坐标公式是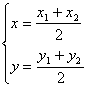 . .3.直线的倾斜角和斜率的关系 (1)每一条直线都有倾斜角,但不一定有斜率. (2)斜率存在的直线,其斜率 4.确定直线方程需要有两个互相独立的条件。直线方程的形式很多,但必须注意各种形式的直线方程的适用范围.
5.两条直线的夹角。当两直线的斜率 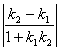 ,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别. ,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别.6.怎么判断两直线是否平行或垂直?判断两直线是否平行或垂直时,若两直线的斜率都存在,可以用斜率的关系来判断;若直线的斜率不存在,则必须用一般式的平行垂直条件来判断. (1)斜率存在且不重合的两条直线 ① ② (2)对于直线 ① ② ③ ④ 7.点到直线的距离公式. (1)已知一点P( (2)两平行直线 8.确定圆方程需要有三个互相独立的条件。圆的方程有两种形式,要知道两种形式之间的相互转化及相互联系 (1)圆的标准方程: (2)圆的一般方程: 二、疑难知识导析 1.直线与圆的位置关系的判定方法. (1)方法一 直线: 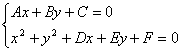  (2)方法二 直线: d=  2.两圆的位置关系的判定方法. 设两圆圆心分别为O1、O2,半径分别为 |O1O2|> |O1O2|= | | O1O2 |=| 0<| O1O2|<| 三、经典例题导讲 [例1]直线l经过P(2,3),且在x,y轴上的截距相等,试求该直线方程. 错解:设直线方程为: ∴直线方程为x+y-5=0. 错因:直线方程的截距式: 正解:在原解的基础上,再补充这样的过程:当直线过(0,0)时,此时斜率为: ∴直线方程为y= 综上可得:所求直线方程为x+y-5=0或y= [例2]已知动点P到y轴的距离的3倍等于它到点A(1,3)的距离的平方,求动点P的轨迹方程. 错解:设动点P坐标为(x,y).由已知3 化简3 当x≥0时得x2-5x+y2-6y+10=0 . ① 当x<0时得x2+ x+y2-6y+10=0 . ② 错因:上述过程清楚点到y轴距离的意义及两点间距离公式,并且正确应用绝对值定义将方程分类化简,但进一步研究化简后的两个方程,配方后得 (x-)2+(y-3)2 = ① 和 (x+)2+(y-3)2 = - ② 两个平方数之和不可能为负数,故方程②的情况不会出现. 正解: 接前面的过程,∵方程①化为(x-)2+(y-3)2 = ,方程②化为(x+)2+(y-3)2 = - ,由于两个平方数之和不可能为负数,故所求动点P的轨迹方程为: (x-)2+(y-3)2 = (x≥0) [例3]m是什么数时,关于x,y的方程(2m2+m-1)x2+(m2-m+2)y2+m+2=0的图象表示一个圆? 错解:欲使方程Ax2+Cy2+F=0表示一个圆,只要A=C≠0, 得2m2+m-1=m2-m+2,即m2+2m-3=0,解得m1=1,m2=-3, ∴当m=1或m=-3时,x2和y2项的系数相等,这时,原方程的图象表示一个圆 错因:A=C,是Ax2+Cy2+F=0表示圆的必要条件,而非充要条件,其充要条件是: A=C≠0且<0. 正解:欲使方程Ax2+Cy2+F=0表示一个圆,只要A=C≠0, 得2m2+m-1=m2-m+2,即m2+2m-3=0,解得m1=1,m2=-3, (1) 当m=1时,方程为2x2+2y2=-3不合题意,舍去. (2) 当m=-3时,方程为14x2+14y2=1,即x2+y2=,原方程的图形表示圆. [例4]自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在的直线方程. 错解:设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3),于是L′过A(-3,-3). 设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0, 已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1 因L′和已知圆相切,则O到L′的距离等于半径r=1 即 整理得12k2-25k+12=0 解得k= 即4x-3y+3=0 因L和L′关于x轴对称 故L的方程为4x+3y+3=0. 错因:漏解 正解:设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3), 于是L′过A(-3,-3). 设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0, 已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1 因L′和已知圆相切,则O到L′的距离等于半径r=1 即 整理得12k2-25k+12=0 解得k= L′的方程为y+3= 即4x-3y+3=0或3x-4y-3=0 因L和L′关于x轴对称 故L的方程为4x+3y+3=0或3x+4y-3=0. [例5]求过直线 (1) 过原点;(2)有最小面积. 解:设所求圆的方程是: 即: (1)因为圆过原点,所以 故所求圆的方程为: (2) 将圆系方程化为标准式,有: 当其半径最小时,圆的面积最小,此时 故满足条件的圆的方程是 点评:(1)直线和圆相交问题,这里应用了曲线系方程,这种解法比较方便;当然也可以待定系数法。(2)面积最小时即圆半径最小。也可用几何意义,即直线与相交弦为直径时圆面积最小. [例6](06年辽宁理科)已知点A( (1)证明线段AB是圆C的直径; (2)当圆C的圆心到直线 解:(1)证明 ∵| 整理得: 设M( 即 整理得: 故线段AB是圆C的直径. (2)设圆C的圆心为C( 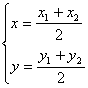 ∵ ∴ 又∵ ∴- ∵ ∴ = 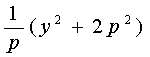 所以圆心的轨迹方程为 设圆心C到直线 = 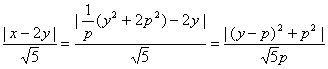 当 ∴ 四、典型习题导练 1.直线  A. B. C. D. 2.已知直线x=a(a>0)和圆(x-1)2+y2=4相切,那么a的值是( ) A.5 B.4 C.3 D.2 3. 如果实数x、y满足等式(x-2)2+y2=3,则 4.设正方形ABCD(A、B、C、D顺时针排列)的外接圆方程为x2+y2-6x+a=0(a<9),C、D点所在直线l的斜率为 (1)求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率; (2)如果在x轴上方的A、B两点在一条以原点为顶点,以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程; (3)如果ABCD的外接圆半径为2 5.如图,已知圆C:(x+4)2+y2=4。圆D的圆心D在y轴上且与圆C外切。圆 D与y轴交于A、B两点,点P为(-3,0). (1)若点D坐标为(0,3),求∠APB的正切值; (2)当点D在y轴上运动时,求∠APB的正切值的最大值; (3)在x轴上是否存在定点Q,当圆D在y轴上运动时,∠AQB是定值?如果存在,求出点Q坐标;如果不存在,说明理由. 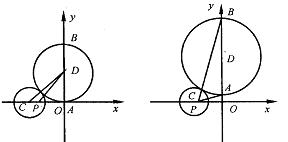 (责任编辑:admin) |
- 上一篇:错解剖析得真知(二十一)
- 下一篇:错解剖析得真知(十二)