错解剖析得真知（二十一）
http://www.newdu.com 2025/05/19 11:05:58 人民教育出版社 佚名 参加讨论
错解剖析得真知（二十一） §7.2圆锥曲线 一、知识导学 1．椭圆定义：在平面内，到两定点距离之和等于定长（定长大于两定点间的距离）的动点的轨迹  2．椭圆的标准方程：  ， （ ）3 椭圆的第二定义:一动点到定点的距离和它到一条定直线的距离的比是一个 内常数 ，那么这个点的轨迹叫做椭圆 其中定点叫做焦点，定直线叫做准线，常数就是离心率椭圆的第二定义与第一定义是等价的，它是椭圆两种不同的定义方式 4．椭圆的准线方程 对于 ，左准线 ；右准线 对于 ，下准线 ；上准线 5.焦点到准线的距离  （焦参数）椭圆的准线方程有两条，这两条准线在椭圆外部，与短轴平行，且关于短轴对称 6 椭圆的参数方程 7．双曲线的定义：平面内到两定点  的距离的差的绝对值为常数（小于 ）的动点的轨迹叫双曲线 即 这两个定点叫做双曲线的焦点，两焦点间的距离叫做焦距8．双曲线的标准方程及特点： （1）双曲线的标准方程有焦点在x轴上和焦点y轴上两种： 焦点在  轴上时双曲线的标准方程为： ( , )；焦点在  轴上时双曲线的标准方程为： (,)(2)  有关系式 成立，且 其中  与b的大小关系:可以为 9 焦点的位置:从椭圆的标准方程不难看出椭圆的焦点位置可由方程中含字母 、 项的分母的大小来确定，分母大的项对应的字母所在的轴就是焦点所在的轴 而双曲线是根据项的正负来判断焦点所在的位置，即项的系数是正的，那么焦点在轴上；项的系数是正的，那么焦点在轴上10．双曲线的几何性质： （1）范围、对称性 由标准方程 ，从横的方向来看，直线x=-,x=之间没有图象，从纵的方向来看，随着x的增大，y的绝对值也无限增大，所以曲线在纵方向上可无限伸展，不像椭圆那样是封闭曲线 双曲线不封闭，但仍称其对称中心为双曲线的中心 （2）顶点 顶点：  ，特殊点： 实轴：  长为2, 叫做半实轴长 虚轴： 长为2b，b叫做虚半轴长双曲线只有两个顶点，而椭圆则有四个顶点，这是两者的又一差异 （3）渐近线 过双曲线 的渐近线 （ ） （4）离心率 双曲线的焦距与实轴长的比  ，叫做双曲线的离心率 范围： 双曲线形状与e的关系：  ，e越大，即渐近线的斜率的绝对值就大，这时双曲线的形状就从扁狭逐渐变得开阔 由此可知，双曲线的离心率越大，它的开口就越阔 11． 双曲线的第二定义：到定点F的距离与到定直线  的距离之比为常数 的点的轨迹是双曲线 其中，定点叫做双曲线的焦点，定直线叫做双曲线的准线 常数e是双曲线的离心率．12．双曲线的准线方程： 对于 来说，相对于左焦点 对应着左准线，相对于右焦点 对应着右准线 ；焦点到准线的距离  （也叫焦参数） 对于 来说，相对于上焦点 对应着上准线 ；相对于下焦点 对应着下准线 抛物线
13 抛物线定义：平面内与一个定点F和一条定直线 的距离相等的点的轨迹叫做抛物线 定点F叫做抛物线的焦点，定直线叫做抛物线的准线 二、疑难知识导析 椭圆、双曲线、抛物线同属于圆锥曲线，它们的定义、标准方程及其推导过程以及简单的几何性质都存在着相似之处，也有着一定的区别,因此，要准确地理解和掌握三种曲线的特点以及它们之间的区别与联系 1．等轴双曲线 定义：实轴和虚轴等长的双曲线叫做等轴双曲线，这样的双曲线叫做等轴双曲线 等轴双曲线的性质：（1）渐近线方程为： ；（2）渐近线互相垂直；（3）离心率 2．共渐近线的双曲线系 如果已知一双曲线的渐近线方程为  ，那么此双曲线方程就一定是： 或写成 3．共轭双曲线 以已知双曲线的实轴为虚轴，虚轴为实轴，这样得到的双曲线称为原双曲线的共轭双曲线 双曲线和它的共轭双曲线的焦点在同一圆上 确定双曲线的共轭双曲线的方法：将1变为-14．抛物线的几何性质 （1）范围 因为p＞0，由方程  可知，这条抛物线上的点M的坐标(x，y)满足不等式x≥0，所以这条抛物线在y轴的右侧；当x的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．（2）对称性 以－y代y，方程 不变，所以这条抛物线关于x轴对称，我们把抛物线的对称轴叫做抛物线的轴．（3）顶点 抛物线和它的轴的交点叫做抛物线的顶点．在方程 中，当y=0时，x=0，因此抛物线的顶点就是坐标原点．（4）离心率 抛物线上的点M与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示．由抛物线的定义可知，e=1． 19 抛物线的焦半径公式：抛物线  ， 抛物线  ， 抛物线  ， 抛物线  ， 三、经典例题导讲 [例1]设双曲线的渐近线为：  ，求其离心率.错解：由双曲线的渐近线为： ，可得： ，从而 剖析：由双曲线的渐近线为 是不能确定焦点的位置在x轴上的，当焦点的位置在y轴上时， ，故本题应有两解，即： 或 .［例2］设点P(x,y)在椭圆  上，求 的最大、最小值.错解：因 ∴ ，得： ，同理得： ，故 ∴最大、最小值分别为3,-3.剖析：本题中x、y除了分别满足以上条件外，还受制约条件 的约束.当x=1时,y此时取不到最大值2,故x+y的最大值不为3.其实本题只需令 ，则 ，故其最大值为 ，最小值为 .［例3］已知双曲线的右准线为  ，右焦点 ,离心率 ,求双曲线方程.错解一：  故所求的双曲线方程为 错解二： 由焦点 知  故所求的双曲线方程为  错因： 这两个解法都是误认为双曲线的中心在原点，而题中并没有告诉中心在原点这个条件。由于判断错误，而造成解法错误。随意增加、遗漏题设条件，都会产生错误解法. 解法一： 设 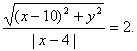 为双曲线上任意一点，因为双曲线的右准线为，右焦点，离心率，由双曲线的定义知 整理得  解法二： 依题意，设双曲线的中心为  ,则  解得 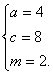 ,所以  故所求双曲线方程为 ［例4］设椭圆的中心是坐标原点，长轴 在轴上，离心率 ，已知点 到这个椭圆上的最远距离是 ，求这个椭圆的方程.错解：依题意可设椭圆方程为  则  ，所以 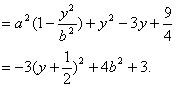 ，即  设椭圆上的点  到点 的距离为 ，则   所以当  时， 有最大值，从而也有最大值。所以  ，由此解得： 于是所求椭圆的方程为  错因：尽管上面解法的最后结果是正确的，但这种解法却是错误的。结果正确只是碰巧而已。由当 时，有最大值，这步推理是错误的，没有考虑到的取值范围.事实上，由于点在椭圆上，所以有 ，因此在求的最大值时，应分类讨论.正解：若  ，则当 时，（从而）有最大值.于是  从而解得 .所以必有  ，此时当时， （从而）有最大值，所以 ，解得于是所求椭圆的方程为 ［例5］从椭圆 ,(>b>0)上一点M向x轴所作垂线恰好通过椭圆的左焦点F1，A、B分别是椭圆长、短轴的端点，AB∥OM设Q是椭圆上任意一点，当QF2⊥AB时，延长QF2与椭圆交于另一点P，若⊿F1PQ的面积为20 ，求此时椭圆的方程解：本题可用待定系数法求解 ∵b=c, = c，可设椭圆方程为 ∵PQ⊥AB,∴kPQ=-  ，则PQ的方程为y=(x-c)，代入椭圆方程整理得5x2-8cx+2c2=0， 根据弦长公式，得  ,又点F1到PQ的距离d=  c∴   ,由 故所求椭圆方程为  ［例6］已知椭圆：  ，过左焦点F作倾斜角为 的直线交椭圆于A、B两点，求弦AB的长解：a=3,b=1,c=2 ; 则F（-2，0）由题意知：  与联立消去y得： 设A（  、B（ ，则 是上面方程的二实根，由违达定理，  ， 又因为A、B、F都是直线上的点，所以|AB|=  点评：也可利用“焦半径”公式计算 ［例7］（06年全国理科）设P是椭圆  短轴的一个端点，Q为椭圆上的一个动点，求｜PQ｜的最大值.解： 依题意可设P（0,1），Q（  ），则｜PQ｜＝ ，又因为Q在椭圆上，所以， ，｜PQ｜2＝ ＝ ＝  .因为  ≤1，＞1，若≥，则 ≤1，当 时，｜PQ｜取最大值 ；若1＜＜，则当 时，｜PQ｜取最大值2.［例8］已知双曲线的中心在原点，过右焦点F（2，0）作斜率为  的直线，交双曲线于M、N 两点，且 =4，求双曲线方程解：设所求双曲线方程为  ，由右焦点为（2，0）知C=2，b2=4-2则双曲线方程为  ，设直线MN的方程为： ，代入双曲线方程整理得：(20-82)x2+122x+54-322=0 设M（x1,y1）,N(x2,y2),则  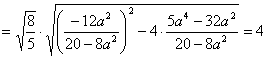，     解得  ， 故所求双曲线方程为：  点评：利用待定系数法求曲线方程，运用一元二次方程的根与系数关系将两根之和与积整体代入，体现了数学的整体思想，也简化了计算，要求学生熟练掌握 四、典型习题导练 1. 设双曲线 两焦点为F1、F2,点Q为双曲线上除顶点外的任一点,过F1作∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹是 （ ）A.椭圆的一部分 B.双曲线的一部分 C.抛物线的一部分 D.圆的一部分. 2．已知点(-2，3)与抛物线y2=2px(p＞0)的焦点 的距离是5，则p= . 3.平面内有两定点  上，求一点P使 取得最大值或最小值，并求出最大值和最小值.4.已知椭圆  的离心率为 .（1）若圆（x-2）2+(y-1)2= 与椭圆相交于A、B两点且线段AB恰为圆的直径，求椭圆方程；（2）设L为过椭圆右焦点F的直线，交椭圆于M、N两点，且L的倾斜角为600，求 的值.5.已知抛物线方程为  ，直线 过抛物线的焦点F且被抛物线截得的弦长为3，求p的值．6.线段AB过x轴正半轴上一点M（m,0）（m>0），端点A、B到x轴距离之积为  ，以x轴为对称轴，过A，O，B三点作抛物线 （1）求抛物线方程； （2）若  的取值范围(责任编辑：admin) |
- 上一篇：错解剖析得真知（二十三）
- 下一篇：错解剖析得真知（二十）