错解剖析得真知(二十二)
http://www.newdu.com 2025/12/23 12:12:04 人民教育出版社 佚名 参加讨论
错解剖析得真知(二十二) §7.3 点、直线和圆锥曲线 一、知识导学 1. 点M(x0,y0)与圆锥曲线C:f(x,y)=0的位置关系 已知 的焦点为F1、F2, 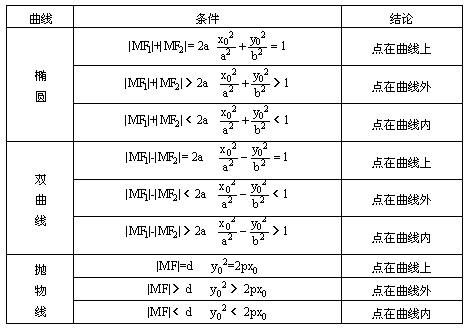 上述结论可以利用定比分点公式,建立两点间的关系进行证明. 2.直线 直线与圆锥曲线的位置关系可分为:相交、相切、相离.对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不是相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.这三种位置关系的判定条件可引导学生归纳为: 设直线 消去y(或消去x)得:ax2+bx+c=0,△=b2-4ac,(若a≠0时), △>0 注意:直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件. 二、疑难知识导析 1.椭圆的焦半径公式:(左焦半径) 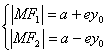 (其中 (其中焦半径公式的两种形式的区别只和焦点的左右有关,而与点在左在右无关 2.双曲线的焦半径 定义:双曲线上任意一点M与双曲线焦点 焦点在x轴上的双曲线的焦半径公式:  焦点在y轴上的双曲线的焦半径公式:  ( 其中 ( 其中3.双曲线的焦点弦: 定义:过焦点的直线割双曲线所成的相交弦。 焦点弦公式: 当双曲线焦点在x轴上时, 过左焦点与左支交于两点时: 过右焦点与右支交于两点时: 当双曲线焦点在y轴上时, 过左焦点与左支交于两点时: 过右焦点与右支交于两点时: 4.双曲线的通径: 定义:过焦点且垂直于对称轴的相交弦 5.直线和抛物线 (1)位置关系: 相交(两个公共点或一个公共点);相离(无公共点);相切(一个公共点). 联立 当 当 若 (2)相交弦长: 弦长公式: 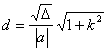 . .(3)焦点弦公式: 抛物线 抛物线 抛物线 抛物线 (4)通径: 定义:过焦点且垂直于对称轴的相交弦 (5)常用结论: 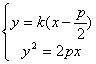 三、经典例题导讲 [例1]求过点 错解: 设所求的过点 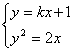 ,消去 ,消去正解: ①当所求直线斜率不存在时,即直线垂直 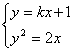 , ,综上,满足条件的直线为: [例2]已知曲线C: 错解:曲线C: 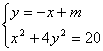 ,得: ,得:错因:方程①与原方程并不等价,应加上 正解:原方程的对应曲线应为椭圆的上半部分.(如图),结合图形易求得m的范围为 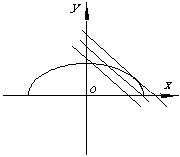 注意:在将方程变形时应时时注意范围的变化,这样才不会出错. [例3]已知双曲线 错解:(1)过点P且与x轴垂直的直线显然不符合要求. (2)设过P的直线方程为 ∴ 解之得:k=2,故直线方程为:y=2x-1,即直线是存在的. 正解:接以上过程,考虑隐含条件“Δ>0”,当k=2时代入方程可知Δ<0,故这样的直线不存在. [例4]已知A、B是圆 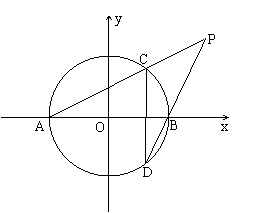  解:由已知得 A (-1, 0 )、B ( 1, 0 ), 设 P ( x, y ), C ( 由A、C、P三点共线得 由D、B、P三点共线得 ①×② 得 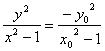 ③ ③又 即点P在双曲线 F ( [例5]已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1 与该椭圆相交于P和Q,且OP⊥OQ,|PQ|= 解:设所求椭圆的方程为 依题意知,点P、Q的坐标满足方程组: 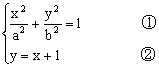 将②代入①,整理得 设方程③的两个根分别为 P( 由题设OP⊥OQ,|OP|= 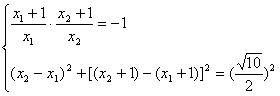 整理得 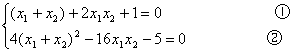 解这个方程组,得 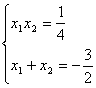 或 或 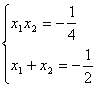 根据根与系数的关系,由③式得 (1) 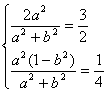 或 (2) 或 (2) 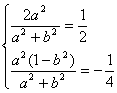 解方程组(1)、(2)得 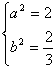 或 或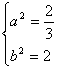 故所求椭圆方程为 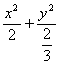 =1 , 或 =1 , 或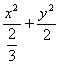 =1. =1.[例6](06年高考湖南)已知椭圆C1:  =1,抛物线C2: =1,抛物线C2:解:(1)当AB⊥ 从而点A的坐标为(1, 因为点A在抛物线上,所以 此时,抛物线C2的焦点坐标为( (1) 当抛物线C2的焦点在直线AB上时,由(1)知直线AB的斜率存在,设直线AB的方程为 (2)  由 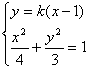 消去 消去设A、B的坐标分别为 ( 则 因为AB既是过C1的右焦点的弦,又是C2的焦点的弦, 所以|AB|=(2- |AB|=( 从而 所以 解得 因为C2的焦点F、( 即 当 当 四、典型习题导练 1.顶点在原点,焦点在x轴上的抛物线被直线l:y=2x+1截得的弦长为 2.直线m:y=kx+1和双曲线x2-y2=1的左支交于A、B两点,直线l过点P(-2,0)和线段AB的中点,则直线l在y轴上的截距b的取值范围为 3. 试求m的取值范围. 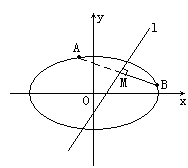 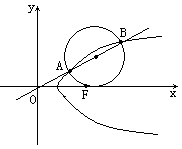 4. 设过原点的直线l与抛物线y2=4(x-1)交于A、B两点,且以AB为直径的圆恰好过抛物线的焦点F, (1)求直线l的方程; (2)求|AB|的长. 5. 如图,过抛物线y2=4x的顶点O作任意两条互相垂直的弦OM、ON,求(1)MN与x轴交点的坐标;(2)求MN中点的轨迹方程. 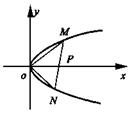 9.设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平行移动t,s单 位长度后得曲线C1. (1)写出曲线C1的方程; (2)证明曲线C与C1关于点A( (3)如果曲线C与C1有且仅有一个公共点,证明s= (责任编辑:admin) |
- 上一篇:错解剖析得真知(二十四)
- 下一篇:错解剖析得真知(二十三)