错解剖析得真知(二十四)
http://www.newdu.com 2025/12/22 08:12:15 人民教育出版社 佚名 参加讨论
错解剖析得真知(二十四) §7.5综合问题选讲 一、知识导学 (一)直线和圆的方程 1.理解直线的斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程. 2.掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式,能够根据直线的方程判断两条直线的位置关系. 3.了解二元一次不等式表示平面区域. 4.了解线性规划的意义,并会简单的应用. 5.了解解析几何的基本思想,了解坐标法. 6.掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程. (二)圆锥曲线方程 1. 掌握椭圆的定义、标准方程和椭圆的简单几何性质. 2. 掌握双曲线的定义、标准方程和双曲线的简单几何性质. 3. 掌握抛物线的定义、标准方程和抛物线的简单几何性质. 4.了解圆锥曲线的初步应用. (三)目标 1.能正确导出由一点和斜率确定的直线的点斜式方程;从直线的点斜式方程出发推导出直线方程的其他形式,斜截式、两点式、截距式;能根据已知条件,熟练地选择恰当的方程形式写出直线的方程,熟练地进行直线方程的不同形式之间的转化,能利用直线的方程来研究与直线有关的问题了. 2.能正确画出二元一次不等式(组)表示的平面区域,知道线性规划的意义,知道线性约束条件、线性目标函数、可行解、可行域、最优解等基本概念,能正确地利用图解法解决线性规划问题,并用之解决简单的实际问题,了解线性规划方法在数学方面的应用;会用线性规划方法解决一些实际问题. 3.理解“曲线的方程”、“方程的曲线”的意义,了解解析几何的基本思想,掌握求曲线的方程的方法. 4.掌握圆的标准方程: 5.正确理解椭圆、双曲线和抛物线的定义,明确焦点、焦距的概念;能根据椭圆、双曲线和抛物线的定义推导它们的标准方程;记住椭圆、双曲线和抛物线的各种标准方程;能根据条件,求出椭圆、双曲线和抛物线的标准方程;掌握椭圆、双曲线和抛物线的几何性质:范围、对称性、顶点、离心率、准线(双曲线的渐近线)等,从而能迅速、正确地画出椭圆、双曲线和抛物线;掌握 二、疑难知识导析 1. ⑴ 直线的斜率是一个非常重要的概念,斜率 ⑵ 直线的截距式是两点式的特例, ⑶求解直线方程的最后结果,如无特别强调,都应写成一般式. ⑷当直线 ⑸在处理有关圆的问题,除了合理选择圆的方程,还要注意圆的对称性等几何性质的运用,这样可以简化计算. 2. ⑴用待定系数法求椭圆的标准方程时,要分清焦点在 ⑵注意椭圆定义、性质的运用,熟练地进行 ⑶求双曲线的标准方程 应注意两个问题:⑴ 正确判断焦点的位置;⑵ 设出标准方程后,运用待定系数法求解. ⑷双曲线 ⑸双曲线的标准方程有两个 ⑹求抛物线的标准方程,要线根据题设判断抛物线的标准方程的类型,再求抛物线的标准方程,要线根据题设判断抛物线的标准方程的类型,再由条件确定参数 三、经典例题导讲 [例1]已知点T是半圆O的直径AB上一点,AB=2、OT= 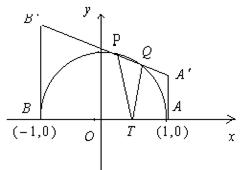 (1)写出直线 (2)计算出点P、Q的坐标; (3)证明:由点P发出的光线,经AB反射后,反射光线通过点Q. 解: (1 ) 显然 (2)由方程组 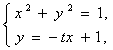 解出 解出 (3) 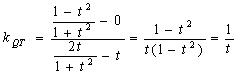 . .由直线PT的斜率和直线QT的斜率互为相反数知,由点P发出的光线经点T反射,反射光线通过点Q. [例2]设P是圆M:( 解:设P( ∴ 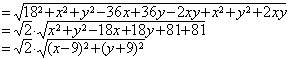 其中 |SQ|的最大值为 [例4](02年天津卷)已知两点M(-1,0),N(1,0)且点P使 (1)点P的轨迹是什么曲线? (2)若点P坐标为 解:(1)记P( 所以 于是, 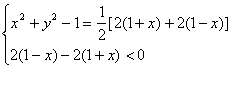 即 即 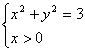 所以,点P的轨迹是以原点为圆心, (2)点P的坐标为 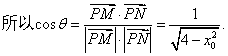 因为 0〈 因为 0〈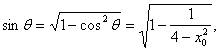 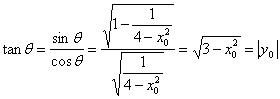 . .[例4]舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度为1千米/秒,炮弹的速度是 分析:答好本题,除要准确地把握好点P的位置(既在线段BC的垂直平分线上,又在以A、B为焦点的抛物线上),还应对方位角的概念掌握清楚. 技巧与方法:通过建立恰当的直角坐标系,将实际问题转化成解析几何问题来求解.对空间物体的定位,一般可利用声音传播的时间差来建立方程. 解:取AB所在直线为 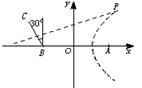 由于B、C同时发现动物信号,记动物所在位置为P,则|PB|=|PC|.于是P在线段BC的中垂线上,易求得其方程为 又由A、B两舰发现动物信号的时间差为4秒,知|PB|-|PA|=4,故知P在双曲线 直线与双曲线的交点为(8,5 据已知两点的斜率公式,得kPA= 设发射炮弹的仰角是θ,初速度v0= ∴sin2θ= 答:方位角北偏东300,仰角30°. 解决圆锥曲线综合题,关键是熟练掌握每一种圆锥曲线的定义、标准方程、图形与几何性质,注意挖掘知识的内在联系及其规律,通过对知识的重新组合,以达到巩固知识、提高能力的目的. (1)对于求曲线方程中参数的取值范围问题,需构造参数满足的不等式,通过求不等式(组)求得参数的取值范围;或建立关于参数的目标函数,转化为函数的值域. (2)对于圆锥曲线的最值问题,解法常有两种:当题目的条件和结论能明显体现几何特征及意义,可考虑利用数形结合法解;当题目的条件和结论能体现一种明确的函数关系,则可先建立目标函数,再求这个函数的最值. [例5]已知抛物线C: (1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线 (2)若M(m,0)是 解:由抛物线 (1)设P( (2)设Q( |MQ|= (ⅰ)当m- (ⅱ)当m- [例6]已知抛物线C的对称轴与 解:设所求抛物线方程为( 由①的顶点到原点的距离为5,得 在①中,令 | 将抛物线①向上平移3个单位,得抛物线的方程为 ( 令 | 依题意得2 即 4( 将抛物线①向左平移1个单位,得( 由抛物线过原点,得(1- 由②③④得 ∴所求抛物线方程为( 四、典型习题导练 1.过抛物线 (1)设点P分有向线段 (2)设直线AB的方程是 2.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大? 3.直线 (1)求实数 (2)是否存在实数 4.已知倾斜角为 (1) 求点B的坐标; (2) 若直线 (3) 对于平面上任一点 5.已知椭圆的中心在原点,离心率为 (1)求椭圆的方程; (2)设Q是椭圆上的一点,且过点F、Q的直线 (责任编辑:admin) |
- 上一篇:错解剖析得真知(二十五)
- 下一篇:错解剖析得真知(二十二)