对称性应用(一)
http://www.newdu.com 2025/12/23 07:12:46 人民教育出版社 佚名 参加讨论
对称性应用(一) ──含绝对值函数的图象 内蒙古赤峰市翁牛特旗乌丹一中 熊明军 在学习函数时,若将函数的自变量或应变量带上绝对值“ 图象是刻画变量之间关系的一个重要途径。函数图象是函数的一种表示形式,是形象直观地研究函数性质的常用方法,是数形结合的基础和依据。本文针对含绝对值函数的性质进行分析,然后利用对称性作出函数图象,并借助图象来展示绝对值对函数性质特征的影响。 一、含绝对值的函数常见情况的分类: 已知函数 ①对自变量 ③对 ⑤对 二、分析不同情况含绝对值函数的性质特点及图象作法: ①对自变量 【特征分析:】 已知函数 【作图步骤:】 (1)作出函数 (2)保留 (3)当 【作图展示:】作函数 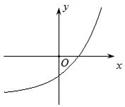 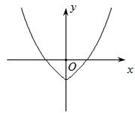 ②对应变量 【特征分析:】 已知函数 【作图步骤:】 (1)作出函数 (2)保留 (3)当 【作图展示:】作函数 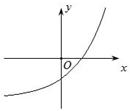 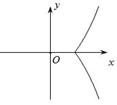 ③对 【特征分析:】 已知函数 【作图步骤:】 (1)作出函数 (2)保留 (3)利用对称性作出(2)中图象关于 【作图展示:】作函数 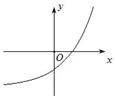 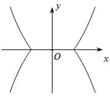 ④对整个函数取绝对值: 【特征分析:】 已知函数 【作图步骤:】 (1)做出 (2)保留 (3)当 【作图展示:】作函数 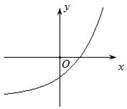 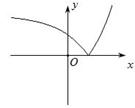 ⑤对 【特征分析:】 已知函数 【作图步骤:】 (1)利用 (2)利用 【作图展示:】作函数  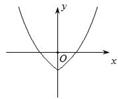 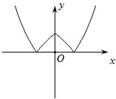 ⑥部分自变量取绝对值: 【特征分析:】已知函数 (责任编辑:admin) |
- 上一篇:错解剖析得真知(二十六)
- 下一篇:错解剖析得真知(二十五)