错解剖析得真知（二十六）
http://www.newdu.com 2025/05/19 08:05:48 人民教育出版社 佚名 参加讨论
错解剖析得真知（二十六） §8.2平面向量与代数、几何的综合应用 一、知识导学 1.余弦定理：三角形任何一边的平方等于其他两边平方的和，减去这两边与它们夹角的余弦的积的2倍,即    2.正弦定理 在一个三角形中，各边和它所对角的正弦的比相等，并且都等于外接圆的直径，即  二、疑难知识导析 1．初中学过的勾股定理只是余弦定理的一种特殊情况。如当  = 时， =0，此时有 ；2．由于本节内容与代数、几何联系比较紧，故读者需对解斜三角形、解析几何中的圆锥曲线等知识非常熟悉方可。 三 经典例题导讲 [例1]在ABC中，已知a2＝b2＋bc＋c2，则角A为( ) A．  B． C． D．或错解：选A 错因：公式记不牢，误将余弦定理中的“减”记作“加”。 正解：∵a2＝b2＋bc＋c2＝b2＋c2－2bc(－  )＝b2＋c2－2bc·cos∴∠A＝ 选 C. [例2]在△ABC中，已知  ，试判别其形状。错解：等腰三角形。 错因：忽视了两角互补，正弦值也相等的情形。直接由 得， ，即 ，则 。接着下结论，所求三角形为等腰三角形正解：由 得，，即则 或 ，故三角形为直角三角形或等腰三角形。[例3]在  中 ，试求周长的最大值。并判断此时三角形的形状。错解：由于题目中出现了角和对边，故使用余弦定理，进一步想使用不等式或二次函数求最值 错因：其实这种思路从表面上看是可行的，实际上处理过程中回遇到无法进行下去的困难。 正解：由正弦定理,得a=2(  )sinA, b=2()sinB.a+b=2( )(sinA+sinB)=4()sin cos sin =sin75o= a+b=( )2 cos≤()2=8+4 .当a=b时,三角形周长最大,最大值为8+4 +. 此时三角形为等腰三角形.[例4]在 中， ，其内切圆面积为 ，求面积。分析：题中涉及到内切圆，而内切圆直接与正弦定理联系起来了，同时正弦定理和余弦定理又由边联系起来了。 解：由已知,得内切圆半径为2 . 由余弦定理,得三角形三边分别为16,10,14.[例5]已知定点A(2,1)与定直线  :3x-y+5=0,点B在上移动,点M在线段AB上,且分AB的比为2,求点M的轨迹方程.分析:向量的坐标为用“数”的运算处理“形”的问题搭起了桥梁,形成了代数与几何联系的新纽带 . 解:设B(x0,y0),M(x,y) ∴  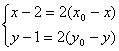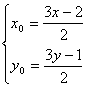=(x-2,y-1), =(x0-x,y0-y),由题知=2∴    由于3x0-y0+5=0,∴3×  - +5=0化简得M的轨迹方程为9x-3y+5=0 [例6]过抛物线:y2=2px(p>0)顶点O作两条互相垂直的弦OA、OB(如图),求证:直线AB过一定点,并求出这一定点. 分析: 对于向量a=(x1,y1),b=(x2,y2),有a//b 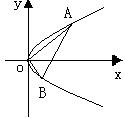 x1y2-x2y1=0.可以用来处理解析几何中的三点共线与两直线平行问题. 证明:由题意知可设A点坐标为(  ,t1),B点坐标为( ,t2) ∴ =(,t1),  =(,t2),∵OA⊥OB,∴ ?=0?+t1?t2=0t1?t2=-4p2 ①设直线AB过点M(a,b),则  =(a-,b-t2), =(-,t1-t2),由于向量 与是共线向量,∴（a-）(t1-t2)= (b-t2)(-) 化简得2p(a-2p)=b(t1+t2) 显然当a=2p,b=0时等式对任意的成立 ∴直线AB过定点,且定点坐标为M(2p,0) 四 典型习题导练 1．已知锐角三角形的边长分别为2，3，x，则第三边x的取值范围是（ ） A．1＜x＜5 B．  ＜x＜ C．＜x＜5 D．1＜x＜2． 三顶点 ，则的面积为__ _。3．△ABC中，若边a：b：c＝  ：(1＋ )：2，则内角A＝ 。4．某人在C点测得塔顶A在南偏西80°，仰角为45°，此人沿南偏东40°方向前进10米到0，测得塔顶A仰角为30°，则塔高＝ 。 5．在△ABC中，已知B＝30°，b＝50  ，c＝150，解三角形并判断三角形的形状。 6．在△ABC中，已知  ＝ ，判定△ABC是什么三角形。※§8.3空间向量及其运算 一、知识导学 1 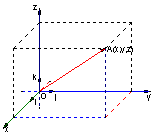 空间直角坐标系：（1）若空间的一个基底的三个基向量互相垂直，且长为 ，这个基底叫单位正交基底，用 表示；（2）在空间选定一点 和一个单位正交基底，以点为原点，分别以 的方向为正方向建立三条数轴： 轴、 轴、 轴，它们都叫坐标轴．我们称建立了一个空间直角坐标系 ，点叫原点，向量 都叫坐标向量．通过每两个坐标轴的平面叫坐标平面，分别称为 平面， 平面， 平面； 2．空间直角坐标系中的坐标： 在空间直角坐标系 中，对空间任一点 ，存在唯一的有序实数组 ，使 ，有序实数组叫作向量在空间直角坐标系中的坐标，记作 ，叫横坐标，叫纵坐标，叫竖坐标．3．空间向量的直角坐标运算律：（1）若  ， ，则  ， ， ， ， ， ．（2）若  ， ，则 ．一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标 4 模长公式：若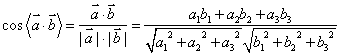， 则 ．5．夹角公式：  ．6．两点间的距离公式：若  ， ，则 二、疑难知识导学 1.对于这部分的一些知识点，读者可以对照平面向量的知识，看哪些知识可以直接推广，哪些需要作修改，哪些不能用的，稍作整理，以便于记忆； 2.空间向量作为新加入的内容，在处理空间问题中具有相当的优越性，比原来处理空间问题的方法更有灵活性，所以本节的学习难点在于掌握应用空间向量的常用技巧与方法，特别是体会其中的转化的思想方法．如把立体几何中的线面关系问题及求角求距离问题转化为用向量解决，如何取向量或建立空间坐标系，找到所论证的平行垂直等关系，所求的角和距离用向量怎样来表达是问题的关键． 3.向量运算的主要应用在于如下几个方面： (1)判断空间两条直线平行(共线)或垂直； (2)求空间两点间的距离； (3)求两条异面直线所成的角. 4.本节内容对于立体几何的应用，读者需自行复习，这里不再赘述。 三、经典例题导讲 [例1]下列所表示的空间直角坐标系的直观图中，不正确的是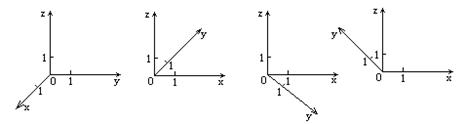（ ）    错解：B、C、D中任选一个 错因：对于空间直角坐标系的表示不清楚。有共同的原点，且两两垂直的三条数轴，只要符合右手系的规定，就可以作为空间直角坐标系． 正解：易知(C)不符合右手系的规定，应选(C)． [例2]已知点A(－3，－1，1)，点B(－2，2，3)，在Ox、Oy、Oz轴上分别取点L、M、N，使它们与A、B两点等距离． 错因：对于坐标轴上点的坐标特征不明；使用方程解题的思想意识不够。 分析：设Ox轴上的点L的坐标为(x，0，0)，由题意可得关于x的一元方程，从而解得x的值．类似可求得点M、N的坐标． 解：设L、M、N的坐标分别为(x，0，0)、(0，y，0)、(0，0，z)． 由题意，得 (x＋3)2＋1＋1＝(x＋2)2＋4＋9， 9＋(y＋1)2＋1＝4＋(y－2)2＋9， 9＋1＋(z－1)2＝4＋4＋(z－3)2． 分别解得  ，故  评注：空间两点的距离公式是平面内两点的距离公式的推广：若点P、Q的坐标分别为(x1，y1，z1)、(x2，y2，z2)，则P、Q的距离为  必须熟练掌握这个公式． [例3]设 ，，且 ，记 ，求 与轴正方向的夹角的余弦值错解：取 轴上的任一向量 ，设所求夹角为 ，∵  ∴   ，即余弦值为  错因：审题不清。没有看清“ 轴正方向”，并不是轴正解：取 轴正方向的任一向量，设所求夹角为，∵ ∴ ，即为所求[例4]在ΔABC中，已知  ＝(2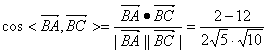,4,0), ＝(－1,3,0)，则∠ABC＝＿＿＿解：   = ∴∠ABC＝135° [例5]已知空间三点A(0,2,3),B(－2,1,6),C(1,－1,5)， ⑴求以向量  为一组邻边的平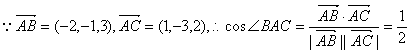行四边形的面积S；⑵若向量  分别与向量垂直，且||＝，求向量的坐标分析：⑴  ∴∠BAC＝60°，  ⑵设 ＝(x,y,z)，则  解得x＝y＝z＝1或x＝y＝z＝－1，∴ ＝(1,1,1)或＝(－1，－1，－1).[例6]已知正方体  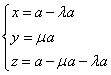的棱长为 ， 是 的中点，是对角线 的中点，求异面直线 和的距离解：以  为原点， 所在的直线分别为轴，轴、轴建立空间直角坐标系，则   ，设  ，∵ 在平面 上，∴  ，即 ，∴  ，∵  ，∴ ，解得：  ，∴ ，∴ ．另外,此题也可直接求  与 间的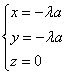距离设 与的公垂线为 ，且 ，设  ，设 ，则  ，∴ ，∴ ，同理  ，∴  ，∴ ，∴  ，解得：  ，  ， ．四、典型习题导练 1．已知向量  的夹角为（ ）A．0° B．45° C．90° D．180° 2．设A、B、C、D是空间不共面的四点，且满足  则△BCD是（ ） A．钝角三角形 B．直角三角形 C．锐角三角形 D．不确定 3．已知  是空间二向量，若 的夹角为 .4．已知点G是△ABC的重心，O是空间任一点，若  为. 5．直三棱柱ABC—A1B1C1中，BC1⊥AB1，BC1⊥A1C 求证：AB1=A1C 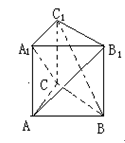 6．如图，直三棱柱ABC—A1B1C1，底面△ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1，A1A的中点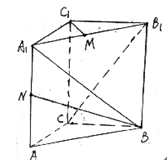，  （1）求  （2）求  （3）  (责任编辑：admin) |