对称性应用（二）_高中学习网-人民教育出版社人教版部编同步解析与测评答案-电子课本资料下载-知识点学习方法与技巧补课解题技巧学习计划表总结-人教网-高中试卷网题库网-中学学科网

对称性应用（二）

http://www.newdu.com 2025/05/19 09:05:30 人民教育出版社佚名参加讨论

    对称性应用（二）
    内蒙古赤峰市翁牛特旗乌丹一中　熊明军
    在高中阶段，函数是数学的主干知识和重要内容，图象是刻画变量之间关系的一个重要途径。函数图象是函数的一种表示形式，是形象直观地研究函数性质的常用方法，是数形结合的基础和依据。本文针对“对称”这个函数的基本性质，利用函数自身的对称和不同函数之间的对称来探讨其对作函数图象的巨大帮助。
    （1）一个函数图象自身关于点对称：
    ①函数关于点对称；
    ②函数关于原点对称；
    ③函数关于轴上的点对称；
    ④函数关于轴上的点对称。
    （2）两个不同函数图象关于点对称：
    ①函数与函数关于任意点对称；
    ②函数与函数关于原点对称；
    ③函数与函数关于轴上的点对称；
    ④函数与函数关于轴上的点对称。
    以上分类，无论函数图象自身关于点对称还是不同函数图象之间关于点对称，若是不结合函数的其它性质，则对用数形结合解决函数图象问题没有多大帮助。因此，在此只列出分类而不加以更多应用的阐明。
    （3）一个函数图象自身关于直线对称：
    ①函数关于直线对称；
    ②函数关于（轴）对称。
    （4）两个不同函数图象关于直线对称：
    ①函数与函数关于直线对称；
    特例：函数与函数关于直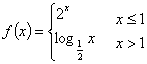线对称；
    ②函数与函数关于直线对称；
    特例：函数与函数关于直线对称（互为反函数）；
    ③函数与函数关于直线对称。
    【例题：】若函数，尝试作出函数的图象。
    【解析：】由函数的对称性知道函数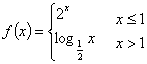与函数关于直线对称，首先，我们作出函数的图象：

然后，利用图像关于直线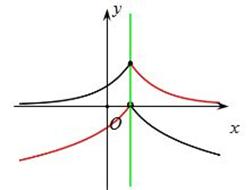对称作出函数图象（红线）：

最后，得函数图象为：

不用求新函数的解析式，直接利用对称性解题，会给许多函数问题的解决带来极大的方便。
(责任编辑：admin)

对称性应用（二）

http://www.newdu.com 2025/05/19 09:05:30 人民教育出版社 佚名 参加讨论

http://www.newdu.com 2025/05/19 09:05:30 人民教育出版社佚名参加讨论