寻求二元一次不等式（组）所表示的平面区域的方法
http://www.newdu.com 2025/05/19 07:05:19 人民教育出版社 佚名 参加讨论
寻求二元一次不等式（组）所表示的平面区域的方法 东北师范大学 熊明军 大连理工大学 曾玲莉 简单线性规划问题是高考必考知识点，而其基础在于研究二元一次不等式（组）所对应的平面区域．下面介绍一些方法来快速准确地确定二元一次不等式（组）所表示的平面区域． 方法一：直线定界，特殊点定域 找出一个二元一次不等式（组）在平面直角坐标系内所表示的平面区域的基本方法是： ①画直线  ②取特殊点③代值定域④求公共部分①画直线──作出各不等式对应方程表示的直线（原不等式带等号的作实线，否则作虚线）； ②取特殊点──平面直角坐标系内的直线要么过原点，要么不过原点；当直线过原点时我们选取特殊点  或 （坐标轴上的点），当直线不过原点时我们选取原点 做特殊点；③代值定域──将选取的特殊点代入所给不等式：如果不等式成立，则不等式所表示的平面区域就是该特殊点所在的区域；如果不等式不成立，则不等式所表示的平面区域就是该特殊点所在区域的另一边． ④求公共部分──不等式组所确定的平面区域，是各个二元一次不等式所表示平面区域的公共部分． 例1 画出不等式组  所表示的平面区域．解析：①画直线：不等式 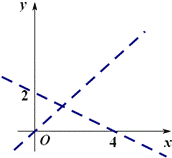 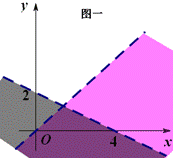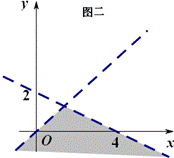对应的直线方程是 ；不等式 对应的直线方程是 ；在平面直角坐标系中作出直线与（如图）．   ②取特殊点：直线 过原点，可取特殊点 ；直线不过原点，可取特殊点 ．③将 代入，即 ，不等式不成立，直线另一侧区域就是不等式所表示的平面区域；将代入，即 ，不等式成立，则原点所在区域就是不等式所表示的平面区域．（图一）④求公共部分：如图二所示公共部分就是不等式组所表示的平面区域． 方法二：法向量判定法 由平面解析几何知识知道直线  （ 不同时为0）的一个法向量为 ．以坐标原点作为法向量的始点，可以利用向量内积证明如下结论：（1）不等式  （ ），不等式表示的平面区域就是法向量指向的区域；（大于同向）（2）不等式  （ ），不等式表示的平面区域就是法向量反向的区域；（小于反向）例2 画出不等式组 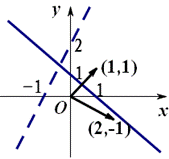 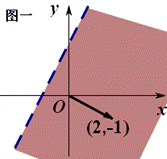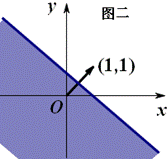所表示的平面区域．解析：①不等式  对应的直线方程是 ，法向量 ；不等式 对应的直线方程是 ，法向量 ；在平面直角坐标系中作出直线与及其相应的法向量（如图）．   ②由于不等式 （ ），平面区域是法向量指向的区域（图一）；不等式（），平面区域是法向量反向的区域（图二）．③然后求的公共部分就是不等式组所表示的平面区域． 方法三：未知数系数化正法 直线 （不同时为0）含有两个未知数，于是我们可以将未知数的系数分为两类： 项系数与 项系数来研究．（1） 项系数化正法：顾名思义就是利用不等式性质，不等号两边同时 （移项）将项系数化为正值，然后根据变形后关于的不等式中的不等号来确定区域位置（规定：轴正方向所指的区域为直线的上方；反之为下方）有结论：项系数正值化： 上； 下．例3 画出不等式组 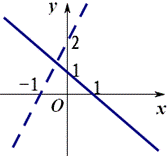 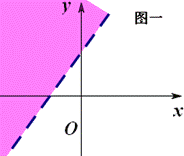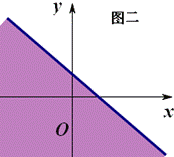所表示的平面区域．解析：①不等式  对应的直线方程是；不等式对应的直线方程是；在平面直角坐标系中作出直线与（如图）．   ②将不等式组中每个不等式 项系数正值化，得 或 （移项）．③关于 的不等式（）即 （或者 ），直线上方的区域就是该不等式所表示的平面区域（图一）；关于的不等式（）即，直线下方的区域就是该不等式所表示的平面区域（图二）．④然后求的公共部分就是不等式组所表示的平面区域． （2） 项系数化正法：同（1）一样，不等号两边同时（或移项）将项系数化为正值，然后根据变形后关于的不等式中的不等号来确定区域位置（规定：轴正方向所指的区域为直线的右方；反之为左方）有结论：项系数正值化： 右； 左．可结合例3来对 项系数化正法进行理解．上述方法中，方法一是寻找二元一次不等式所表示的平面区域的常规方法，思维回路较长，适合对理论的学习，但要快速准确地解决简单的线性规划问题就必须掌握方法二或方法三中之一． (责任编辑：admin) |
- 上一篇：直观图中的面积问题
- 下一篇：巧思妙解论坛里的一个问题