9、如图9-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。
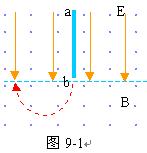
分析与解:(1)带电小球在沿杆向下运动时,其受力情况如9-2图示。
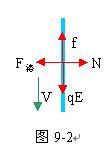
水平方向:F洛=N=qBV [1]
竖直方向:qE=f [2] (匀速运动时)
又因f=μN [3],联立解[1][2][3]式得:qE=f=μqBVb
小球在磁场中作匀速圆周运动:qBVb=mVb2/R=3mVb2/L,所以Vb=qBL/3m
小球从a到b运动过程中,由动能定理:W电-Wf=(1/2)mVb2
W电=qEL=μqBVbL=0.3×qBL(qBL/3m)=q2B2L2/10m
所以,Wf=W电-(1/2)mVb2=q2B2L2/10m-(m/2)(q2B2L2/9m2)=2q2B2L2/45m
所以,Wf/W电=(2q2B2L2/45m)/(q2B2L2/10m)=4/9。
10、如图10-1所示,从阴极K射出的电子经U0=5000V的电势差加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之间。在离金属板边缘L2=75cm处放置一个直径D=20cm,带有记录纸的圆筒。整个装置放在真空内,电子发射的初速度不计。
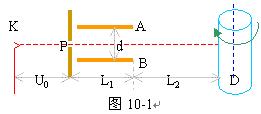
(1)若在金属板上加以U1=1000V的直流电压(A板电势高)后,为使电子沿入射方向作匀速直线运动到达圆筒,应加怎样的磁场(大小和方向);
(2)若在两金属板上加以U2=1000cos2πtV的交流电压,并使圆筒绕中心轴按图示方向以n=2转/秒匀速转动。试确定电子在记录纸上的轨迹形状,并画出1秒钟内所记录到的图形。
分析与解:偏转极板上加恒定电压 U后,电子在电场中受到恒定的电场力作用,故所加的磁场方向只要使运动电子所受到的洛仑兹力与电场力等大反向即可。偏转极板上加上正弦交流电后,板间电场变为交变电场,电子在板间的运动是水平方向作匀速直线运动,竖直方向作简谐运动。偏出极板后作匀速直线运动,电子到达圆筒后,在筒上留下的痕迹是电子在竖直方向的“扫描”和圆筒匀速转动的合运动。
据动能定理:eU0=(1/2)mV02,得电子加速后的入射速度为:
V0=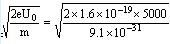 =4.2×107m/s =4.2×107m/s
(1)加直流电压时,A、B两板间场强:
E1=U1/d=1000/(4×10-2)=2.5×104v/m
为使电子作匀速直线运动,应使电子所受电场力与洛仑兹力平衡,
即:qE1=qBV0,
得:B=E1/V0=(2.5×104)/(4.2×107)=6×10-4T
方向为垂直于纸面向里。
(2)加上交流电压时,A、B两板间场强为:
E2=U2/d=1000cos2πt/(4×10-2)=2.5×104cos2πt v/m
电子飞离金属板时的偏距为:y1=(1/2)at12=(1/2)(eE2/m)(L1/V0)2
电子飞离金属板时的竖直速度为:Vy=at1=(eE2/m)(L1/V0)
从飞离板到到达筒的偏距:y2=Vyt2=(eE2/m)(L1/V0)(L2/V0)=(eE2L1L2)/(mV02)
所以在纸筒上的落点对入射方向的总偏距为:(如图10-2所示)
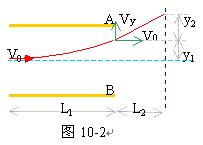
y=y1+y2=(L1/2+L2)(eE2L1/mV02)=(L1/2+L2)(L1U2/2U0d)
=(10/2+75)×10-2×(10×1000cos2πt)/(2×5000×4)=0.20cos2πt m
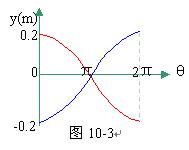
可见,在记录纸上的点以振幅0.20m,周期T=2π/ω=1秒而作简谐运动。因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图10-3所示。
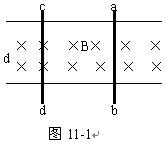
11、如图11-1所示,两根互相平行、间距d=0.4米的金属导轨,水平放置于匀强磁场中,磁感应强度B=0.2T,磁场垂直于导轨平面,金属滑杆ab、cd所受摩擦力均为f=0.2N。两根杆电阻均为r=0.1Ω,导轨电阻不计,当ab杆受力F=0.4N的恒力作用时,ab杆以V1做匀速直线运动,cd杆以V2做匀速直线运动,求速度差(V1- V2)等于多少?
分析与解:在电磁感应现象中,若回中的感应电动势是由导体做切割磁感线运动而产生的,则通常用ε=BlVsinθ来求ε较方便,但有时回路中的电动势是由几根棒同时做切割磁感线运动产生的,如果先求出每根导体棒各自的电动势,再求回路的总电动势,有时就会涉及“反电动势”而超纲。如果取整个回路为研究对象,直接将法拉第电磁感应定律ε=
11、如图11-1所示,两根互相平行、间距d=0.4米的金属导轨,水平放置于匀强磁场中,磁感应强度B=0.2T,磁场垂直于导轨平面,金属滑杆ab、cd所受摩擦力均为f=0.2N。两根杆电阻均为r=0.1Ω,导轨电阻不计,当ab杆受力F=0.4N的恒力作用时,ab杆以V1做匀速直线运动,cd杆以V2做匀速直线运动,求速度差(V1- V2)等于多少?
分析与解:在电磁感应现象中,若回中的感应电动势是由导体做切割磁感线运动而产生的,则通常用ε=BlVsinθ来求ε较方便,但有时回路中的电动势是由几根棒同时做切割磁感线运动产生的,如果先求出每根导体棒各自的电动势,再求回路的总电动势,有时就会涉及“反电动势”而超纲。如果取整个回路为研究对象,直接将法拉第电磁感应定律ε=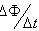 用于整个回路上,即可“一次性”求得回路的总电动势,避开超纲总而化纲外为纲内。 用于整个回路上,即可“一次性”求得回路的总电动势,避开超纲总而化纲外为纲内。
cd棒匀速向右运动时,所受摩擦力f方向水平向左,则安培力Fcd方向水平向右,由左手定则可得电流方向从c到d,且有:
Fcd = IdB = f
I = f /Bd ①
取整个回路abcd为研究对象,设回路的总电势为ε,由法拉第电磁感应定律
ε=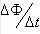 ,根据B不变,则△φ=B△S,在△t时间内, ,根据B不变,则△φ=B△S,在△t时间内,
△φ=B(V1-V2)△td
所以:ε=B(V1-V2)△td/△t=B(V1-V2)d ②
又根据闭合电路欧母定律有:I=ε/2r ③
由式①②③得:V1-V2 = 2fr / B2d2
代入数据解得:V1-V2 =6.25(m/s)
12.如图12-1所示,线圈abcd每边长l=0.20m,线圈质量m1=0.10kg、电阻R=0.10Ω,砝码质量m2=0.14kg.线圈上方的匀强磁场磁感强度B=0.5T,方向垂直线圈平面向里,磁场区域的宽度为h=l=0.20m.砝码从某一位置下降,使ab边进入磁场开始做匀速运动.求线圈做匀速运动的速度.
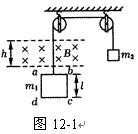
解析:该题的研究对象为线圈,线圈在匀速上升时受到的安培力F安、绳子的拉力F和重力m1g相互平衡,即
F=F安+m1g. ①
砝码受力也平衡:
F=m2g. ②
线圈匀速上升,在线圈中产生的感应电流
I=Blv/R, ③
因此线圈受到向下的安培力
F安=BIl. ④
联解①②③④式得v=(m2-m1)gR/B2l2.
代入数据解得:v=4(m/s)
13.如图13-1所示,AB、CD是两根足够长的固定平行金属导轨,两导轨间距离为l,导轨平面与水平面的夹角为θ.在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感强度为B.在导轨的A、C端连接一个阻值为R的电阻.一根垂直于导轨放置的金属棒ab,质量为m,从静止开始沿导轨下滑.求ab棒的最大速度.(已知ab和导轨间的动摩擦因数为μ,导轨和金属棒的电阻不计)
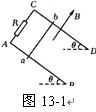
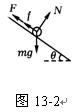
解析:本题的研究对象为ab棒,画出ab棒的平面受力图,如图13-2.ab棒所受安培力F沿斜面向上,大小为F=BIl=B2l2v/R,则ab棒下滑的加速度
a=[mgsinθ-(μmgcosθ+F)]/m.
ab棒由静止开始下滑,速度v不断增大,安培力F也增大,加速度a减小.当a=0时达到稳定状态,此后ab棒做匀速运动,速度达最大.
mgsinθ-(μmgcosθ+B2l2v/R)=0.
解得ab棒的最大速度
vm=mgR(sinθ-μcosθ)/B2l2.
(责任编辑:admin)
|