在各地中考试题中,都有一些难度较大、技巧性很强的计算类选择题.这类题目按常规物理解题方法,需列出数个物理关系式,然后借助数学技巧(如比例性质、不等式性质、分式性质等)进行推导演算才能解答.但是,由于初中学生的数学技巧欠缺,在解答这类题目时正确率很低.而用赋值分析求解这类题,就能达到快速准确的目的.下面举例说明.
例1 甲、乙两同学同时从A地到B地,甲在全程的时间内一半时间跑,一半时间走;而乙在全程内一半路程跑,一半路程走,若他们跑和走的速度分别对应相同,则().
A.甲先到B地
B.乙先到B地
C.他们同时到B地
D.无法确定
解析 赋值:A、B两地相距s=400米,跑的速度v1=8米/秒,走的速度v2=2米/秒.设甲用时间t甲,乙用时间t乙,由题义可知:
甲同学:s=(t甲/2)v1+(t甲/2)v2,
解得 t甲=80秒.
乙同学:t乙=(s/2)/v1+(s/2)/v2,
解得 t乙=125秒.
显然 t甲<t乙,故答案选取A项.
例2 如图1所示,两只溢水杯分别盛满甲、乙两种液体,把一小球放入甲液体中,小球沉入杯底,溢出液体30克;把完全相同的另一小球投入乙液体中,小球漂浮在液面上,溢出液体40克,则甲、乙两种液体的密度之比ρ甲∶ρ乙为().
A.小于3∶4
B.等于3∶4
C.大于3∶4
D.不能确定
解析 赋值:设小球体积为V,乙中小球排开液体的体积V排=V/2.则由密度知识可知,ρ甲=30/V,ρ乙=40/V排=80/V,
所以ρ甲∶ρ乙=3∶8<3∶4.
故答案应为选项A.
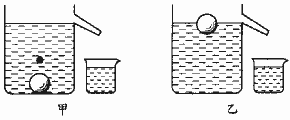
图1
例3 三个完全相同的长方体木块,分别放入三种密度不同的液体中,木块均漂浮,如图2所示.甲木块大部分浸入液体中,乙木块刚好一半浸入液体中,丙木块小部分浸入液体中.若将木块露出液面的部分切除后,比较木块再次露出液面部分的体积().
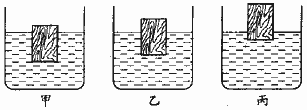
图2
A.甲最大
B.乙最大
C.丙最大
D.一样大
解析 赋值:设甲、乙、丙露出液面的体积分别占总体积的1/3、1/2、3/4,木块的体积为V.由题意,露出液面的部分切除后,再次露出液面的体积占剩余体积的比不变,所以,它们再次露出液面的体积分别为:V甲=2V/9、V乙=V/4、V丙=3V/16.显然V乙最大,故答案应为选项B.
例4 如图3所示,电源电压恒定,已知R1∶R2=2∶1.当开关S闭合时,电流表A1与A2的读数之比为().
A.1∶3
B.3∶1
C.2∶3
D.3∶2
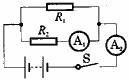
图3
解析 赋值:电源电压U=12伏,R1=12欧,R2=6欧.则通过R1的电流为IR1=U/R1=1安;电流表A1的读数IA1=U/R2=2安;电流表A2的读数为IA2=1安+2安=3安.所以,电流表A1与A2的读数之比为2∶3,故答案为选项C.
例5 如图4所示,当电路中A、B两点间接入10欧的电阻时,电流表的示数为0.5安.若A、B间改接20欧的电阻时,则电流表的示数().
A.等于0.25安
B.小于0.25安
C.大于0.25安
D.无法判定
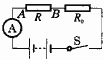
图4
解析 赋值:设R0=5Ω,则电源电压U=0.5安×(10欧+5欧)=7.5伏.当A、B间改接20欧的电阻时,电路中的电流为:
I‘=U/(R’+R0)=7.5/(20+5)=0.3>0.25,
故答案应选取C项.
通过以上几例可见,赋值法解物理选择题快捷且准确.它不仅能使抽象的定量研究具体化,而且还能使一些定性研究的问题定量化,因而易被学生接受.
(责任编辑:admin)
|