2.为训练宇航员能在失重状态下工作和生活,需要创造一种失重的环境。在地球表面附近,当飞机模拟某些在重力作用下的运动时,就可以在飞机座舱内实现短时间的完全失重状态。现要求一架飞机在速率为
答案:(1)做加速度为g的抛体运动,时间与抛出角有关
50s-150s
3.质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上,平衡时,弹簧的压缩量为x0,如图所示,一个物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动,已知物块质量也为m时,它们恰能回到O点,若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度,求物块向上运动到最高点距O点的距离.
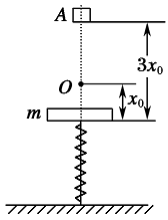
答案:x0/2
4.一质量为M的平顶小车,以速度v
0沿水平的光滑轨道作匀速直线运动。现将一质量为m的小物块无初速地放置在车顶前缘。已知物块和车顶之间的动摩擦系数为
μ。
1. 若要求物块不会从车顶后缘掉下,则该车顶最少要多长?
2. 若车顶长度符合1问中的要求,整个过程中摩擦力共做了多少功?
答案:
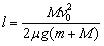
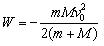
5.试证明行星绕行恒星运动时具有的能量为-GMm/2a,其中M为恒心的质量,m为行星的质量,a为行星轨道半长轴。
答案:
由开普勒第二定律: v
1r
1=v
2r
2 v
1、v
2分别为行星近日点和远日点的速率,r
1,r
2为近日点与远日点时行星与恒心的球心距
mv
12/2-GMm/r
1=mv
22/2-GMm/r
2 =>
v
12- v
22 =2GM/r
1-2GM/r
2 => v
12(1-r
12/r
22) =2GM(1/r
1-1/r
2)
=> v
12(r
22-r
12)/r
22 =2GM(r
2- r
1)/ r
1r
2 => v
12(r
2+r
1)/r
2=2GM/ r
1 由 r
2+r
1=2a 得:
=> v
12a/r
2=GM/ r
1 => v
12=GM r
2/(ar
1)
=>E= mv
12/2-GMm/r
1 =m GM r
2/(2ar
1)-GMm/r
1 = GMm(r
2/(2ar
1)-1/r
1)
= GMm(r
2-2a/(2ar
1)) = GMm(-r
1/(2ar
1)) = -GMm/(2a)
证毕
(责任编辑:admin)