2.
ΔU/n
0=2.86Χ10
5J/mol
3.如图,质量为m
1 的物体A经一轻质弹簧与下方地面上的质量为m
2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连轻挂钩.开始时各段 绳都处于伸直状态,A上方的一段绳沿竖直方向.现在挂钩上挂一质量为m
3的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将C换成另一质量为 (m
1+m
3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度为g.

答案:开始时,A、B静止,设弹簧压缩量为x
1,有 kx
1=m
1g ①
挂C并释放后,C向下运动,A向上运动 ,设B刚要离地时弹簧伸长量为x
2,有
kx
2=m
2g ②
B不再上升,表示此时A和C的速度为零,C已降到最低点.
由机械能守恒,与初始状态相比,弹簧弹性势能的增加量为
ΔE=m
3g (x
1+x
2)— m
1g(x
1+x
2)
C换成D后,当B刚离地时弹簧势能的增量与第一次相同,由能量关系得
(m
3+m
1)v
2/2+m
1v
2/2=(m
3+m
1)g(x
1+x
2) - m
1g(x
1+x
2) – ΔE ④
由③④式得 (2m
1+m
3)v
2/2=m
1g (x
1+x
2) ⑤
由①②⑤式得
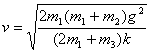
⑥
4.如图所示,倾角为θ的光滑斜面上,一个质量为M、长为L的薄木板被一个受轻质杆约束于光滑轴O的质量为m的重球压住不动.已知重球半径为R,重球球心C到光滑轴O之距离也为L,且轻质杆也沿斜面方向(与斜面平行).现将斜面倾角θ缓缓增加,当增至30°时,薄木板刚好滑动,尔后将斜面倾角突然增至45°且保持不变.试求:
(1)重球与薄木板之间的动摩擦因数μ.
(2)在斜面倾角为45°情况下,薄木板从重球之下滑出所用的时间t.
(3)在斜面倾角为45°情况下,薄木板从重球之下刚刚滑出时的瞬时速度v
t 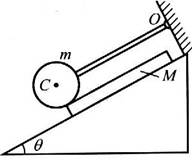
答案:
(1)
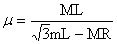
(2)
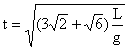
(3)
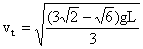
5.一卡车拖挂一相同质量的车厢,在水平直道上以v
0 = 12 m/s的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为a = 2 m/s
2的加速度减速滑行。在车厢脱落t = 3s后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
答案:设卡车的质量为M,车所受阻力与车重之比为μ;刹车前卡车牵引力的大小为F,
卡车刹车前后加速度的大小分别为a
1和a
2。重力加速度大小为g。由牛顿第二定律有
f-2μMg=0 ①
F-2μMg=Ma
1 ②
μMg=Ma ③
3μMg=Ma
2 ④
设车厢脱落后,t=3s内卡车行驶的路程为s
1,末速度为v
1,根据运动学公式有
s
1=v
ot+a
1t
2/2 ⑤
v
1=v
0+a
1t ⑥
v
12=2a
2s
2 ⑦
式中,s
2是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为s,有v
02=2as ⑧
卡车和车厢都停下来后相距 Δs=s1+s2-s ⑨
由①至⑨式得 Δs=-v
02/(3a)+4v
0t/3+2at
2/3 ⑩
带入题给数据得Δs=36m
(责任编辑:admin)