利用化学知识解决地理区位因素问题
http://www.newdu.com 2024/11/23 07:11:19 人民教育出版社 佚名 参加讨论
利用化学知识解决地理区位因素问题 北京四中高二学生 陈曦 指导教师 刘刚 北京四中高二学生 陈曦 朴素的政治理念告诉我们，世界上的万事万物都是有着某种客观的内在联系的。通过在地理和化学学科上个人学习的经历和过程。以及通过地理老师在课上关于地理区位因素与各学科知识联系与建模的启迪，我发现地理学科上有些知识可以用化学模型解释并演算，我浅浅的思考了关于地理区位因素的化学建模，并记于此。有不当之处并请指正。 地理学的研究思想是由浅入深，先建立大体骨架，在向内加入限制条件并不断完善，我也是采取此种方法思考这个问题的。  图 1 在其他条件都理想化或忽略不计的情况下，若▲代表铁矿，那么钢铁工业应建立在A、B、C哪一点呢？毫无疑问应该选距离铁矿最近的一点。这与化学上的不可逆反应极为想象，例如设： aA+Bb 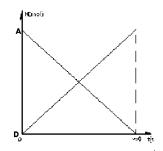 dD+eE 
∵条件理想 ∴简化为 A D
∵不可逆反应 ∴vA≈∞ 图 2 用反应趋势图像（图2）表示（用直线近似表示反应过程）。在速率上的 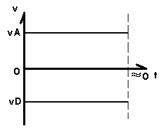 表示成为图3的样子。注意对比两图。在t≈0时已经完成反应，即达到稳态。若以正方向反应参数代表选址趋势，即无限接近于▲。
图 3 但是如此理想的模型在现实生活中不可能存在。所以向内加入影响因素成为必然。首先关注A D，若加入系数，只影响最后结果即稳态的最后状态。在地理学上是指安排好最好区位因素后所获得的收效，显然我们首先需要解决的并不是结果，而是过程，即工农业的选址，也就是稳态时的速率统一。在此模式下，工业选址是极限化的。也就是极限靠近单一优势区位。
看到这里，读者自然会问：如果有双优势区位怎么办呢？更多呢？这里先讨论双区位因素。 
图 4 工厂应建立在哪里呢？（假设其他一切条件理想），如果河流和铁矿对这个工厂的影响是等同的，毫无疑问应建立在铁矿道和最短距离的中点。 若设方程 A D
那么有速率图像如图5。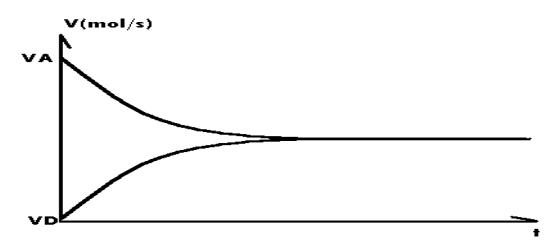 
∵主要讨论区位因素对选址的影响 ∴不考虑收效 ∵在理想状态下，最优区位可获得最大收效。 ∴稳态时，重合处正好在于两者之间。 即稳态时[A]/[B]=1 VA/VB=1 这个“1”。命其名为确定区位系数。 但是读者又会发现，事情并不是这么简单。但就此事来说，工厂的选址并不一定在中点，这里面有多方面的因素需要我们去考虑。例如工厂用矿多，或者矿运费高，则选址必然靠近铁矿。反之用水多，或水的运费高，则靠河。如果假定水和矿的运输成本相同，则工厂靠近水或矿完全可以与用量成比例。这些客观上确定的因素称之为客观因素，即不以人的意志为转移的影响工农业区位在选址上表现的因素。还有一类因素是可以受人影响的，比如，我个人喜欢山，我就把工厂建在铁矿边；反之我个人喜欢游泳，则把工厂建在河边（当然，如果没有污染的话）。这叫做主观因素，这里的客观因素一般是确定且有偏向的，即VA/VB≠1，设确定区位系数为k，则VA/VB=k，而主观因素则就好比改变反应的外部条件，这时化学反应速率方程就已经不太适用了（本身速率方程一般式是VA=k[CA]a[CB]b）,这就是说，速率方程只能计算出稳态时一方面的量。而且此方程和反应物生成物关系并不明显，必然会给我们以后的建模带来麻烦。其实在达到稳态的时候VA=VB，其比必等于1。所以这个模型不太适应，但它有它的作用，我们将在后面引述。 前面还有一个问题没有解决，即最优区位不一定等于最大收效。那么如果我们把方程式加上系数后设aA dD
根据化学平衡反应方程k=[CA]a/[CD]d。这很容易计算出平衡点所在位置，即选址地。 如果在加入其它的影响因素和收效因素，则 aA +bB dD +eE
此时 k=[CA]a[CB]b/[CD]d[CE]e 这时我们就可以利用化学知识，在实际应用中测出集中数据，算出k就可以。再带入各种不可变因素。就可算出最佳选址，或直接利用化学试验模拟。 再谈速率方程。我们知道一些化学反应，它的反应趋势非常大，但反应速度非常小。还有一类化学反应，化学反应趋势非常大，但化学反应速率非常小。在地理学上，或拿到生活中来就是：有的工厂选址是客观因素占主要方面，有的主观因素占主要方面。这是我们讲，因为一般认为客观因素是常数，用平衡方程比较好解释，但主观因素的变化无常，虽然我们可以通过改变k来解释问题，但平衡是相对静止的，而速率是可以易于改变的，所以这就指引着我们用速率方程解决问题。在aA +bB dD +eE中。设V正=j[CA]a[CB]b,V逆=j’[CD]d[CE]e（这可是不一定的，不过也有方便之处）。这两个方程教易于解释变化中的行为。这时的V正代表某地（即某反应时刻）的建立可行性，V逆代表非建立可行性。反应速率并不完全与反应物和生成物挂钩，就好像生活中有些区位不会影响选址过程，只用在结果中加入进去，这里的j显然与确定区位系数k不同，其实二者也是有联系的。当选址确定时（即达到动态平衡），V正= V逆。
j[CA]a[CB]b=j’[CD]d[CE]e k=j’/j 现在就可以定义k为区位客观常数，定义j为区位主观正常数，定义j'为区位主观逆常数。结合图6来看可把主观因素影响下的区位理解为为平衡时（t1）似的情形。并不是说主观因素不该出现的意思，即使不应出现本着地理学和化学客观而实事求是的研究态度，也应该考虑进去。可以理解为工厂选址一旦确定，主观因素的影响就微乎其微了，其只在论证部分发挥作用。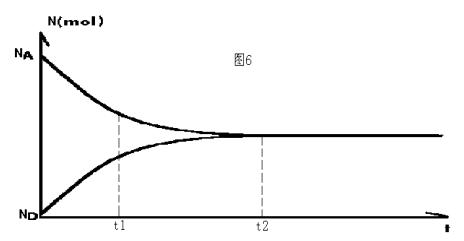 
这样通过数学计算和化学模拟，就可以解决许多区位问题，为地理学提供了定量计算的依据。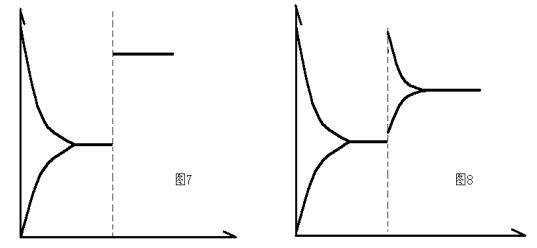 
在工厂迁址时，可以分两种情况，若客观因素改变，可视为添加了催化剂，在平衡的基础上改变选址，如图7，而主观因素占上风时，可视为动态的改变。该图像很好的说明了客观改变有助于企业的发展，而主观改变需要一定时间的磨合。 顺便解释一下，本文的图只是定性的举例说明，若定量分析，需要精确的实验论证。 在工业区等工业地域的建设时，若两个工厂正相关，即互相有推动作用，那么K=k1k2,把两厂或两反应联立，得到图9。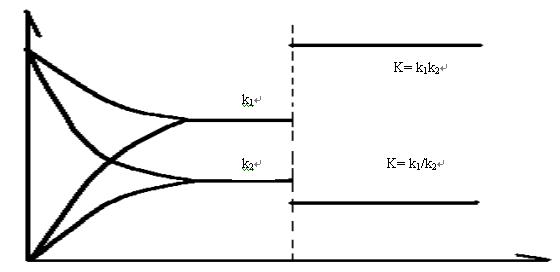 
图 9 若两厂负相关。则K= k1/k2,这样可较方便的解决其问题。 但是美中不足的是，此套理论只属纸上谈兵，没有事实检验，仅供参考。这只是本人的一个想法，不知对否，请老师予以指教。 (责任编辑：admin) |