单摆实验判断单摆习题
江西省南丰一中 聂应才
实践是检验真理的唯一标准,对于物理来说,实验是判断习题正误的依据。当物理习题出现不同答案时,不应该仅是思维上的讨论,而是去实验室做实验,看看实验结果是什么,答案就是什么了。笔者在教学中遇到单摆习题在不同参考资料中答案不同,笔者就带学生们走进实验室,在实验面前结果迎刃而解
【习题一】在利用单摆测定重力速度的实验中,某同学测出了多组摆长和运动周期,根据实验数据,作出T2-l的关系图象如图1所示。
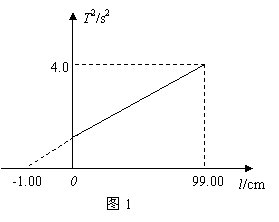
(1)该同学实验中出现的错误可能是_________________________。
(2)虽然实验中出现了错误,但根据图象中的数据,仍可算出准确的重力加速度,其值为_____________m/s2。
在不同的参考资料中,第1问出现了截然不同的两种答案:一个说“测摆长时多加摆球的半径”,一个说“测摆长时漏了摆球的半径”。到底哪个资料讲得是正确的呢?
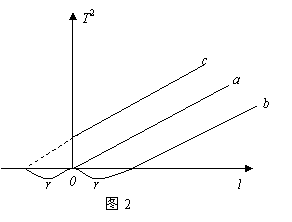
理论分析:当l=0时,其周期不为零,说明图1是漏了摆球的半径,其周期不为零的值正好是摆球半径作为此时的摆长;从另一角度看:周期T是实验测出来的,与漏不漏半径或多加摆球半径无关,所以图1中的纵坐标是确定的,对应横坐标,如果漏了半径,横坐标的值小了,自然向右平移得到图1的图象。但有资料给出如下详细参考答案:当漏测r时,相当于以线长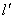 为摆长l,这时 为摆长l,这时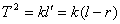 ,从数学知识可知,这时的图象斜率不变(如图2可将原图线a向右平移r,得图中线b,但斜率不变)。同理,当多加r时,图线为c,因此该同学实验中出现的错误是测摆长时多加了摆球的半径。这个分析过程中,回答了第2问是正确的,但在讲解第1问时是不对,写得“雾里看花”。学生看了这个不同的答案很高兴,尽管他们看得很拗口,但是却能等着看教师怎么办。笔者没有在理论上给予更的说明,而是把他们带进了实验室,重做了实验。 ,从数学知识可知,这时的图象斜率不变(如图2可将原图线a向右平移r,得图中线b,但斜率不变)。同理,当多加r时,图线为c,因此该同学实验中出现的错误是测摆长时多加了摆球的半径。这个分析过程中,回答了第2问是正确的,但在讲解第1问时是不对,写得“雾里看花”。学生看了这个不同的答案很高兴,尽管他们看得很拗口,但是却能等着看教师怎么办。笔者没有在理论上给予更的说明,而是把他们带进了实验室,重做了实验。
数据表一(摆球直径为2.00cm)
摆线长/cm
|
47.10
|
58.40
|
68.80
|
74.18
|
88.40
|
95.45
|
周期T/s
|
1.39
|
1.55
|
1.68
|
1.74
|
1.90
|
1.97
|
T2/s2
|
1.93
|
2.40
|
2.82
|
3.03
|
3.61
|
3.88
|
把摆长作为横坐标(以m作为单位),周期的平方作为纵坐标(以s2为单位),每一次摆长对应一个周期即周期的平方,在T2-l中即为一对点。列出表格如下
数据表二
漏了半径
|
(0.4710,1.93)
|
(0.5840,2.40)
|
(0.6880,2.82)
|
(0.7418,3.03)
|
(0.8840,3.61)
|
(0.9545,3.88)
|
加了半径
|
(0.4810,1.93)
|
(0.5940,2.40)
|
(0.6980,2.82)
|
(0.7518,3.03)
|
(0.8940,3.61)
|
(0.9645,3.88)
|
加了直径
|
(0.4910,1.93)
|
(0.6040,2.40)
|
(0.7080,2.82)
|
(0.7618,3.03)
|
(0.9040,3.61)
|
(0.9745,3.88)
|
在坐标纸上标出上述数据,然后用一条直线把相应的点连接起来,得到的结果如图3。

图3 漏半径、加半径、加直径的T2-l图
从图3中直观地发现,这三根直线是靠的很紧得,不象图1或图2那样横坐标的截距有那样的明显,并且这三根直线是相互平行,因此其斜率是一样的,所以习题一的第(1)问应该是漏了半径,尽管漏了半径,但其斜率是准确的,第(2)的重力加速度是准确值,为9.86m/s2。通过这般实验过程,学生对其结果不再有异议了。实验还能给出更多的信息:第一,从图3中观察出纵坐标的截距约为T02=0.04 s2,由公式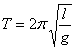 ,得l=0.01m=1.0cm正好是摆球的半径!与理论分析得一致。第二,为什么作T2-l图象斜率与摆球半径无关?因为由 ,得l=0.01m=1.0cm正好是摆球的半径!与理论分析得一致。第二,为什么作T2-l图象斜率与摆球半径无关?因为由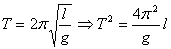 ,l漏加摆球半径r或多加摆球半径r,由数学知识可知,其直线仅是左右平移而已,斜率 ,l漏加摆球半径r或多加摆球半径r,由数学知识可知,其直线仅是左右平移而已,斜率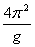 不变。如果是直接由公式 不变。如果是直接由公式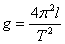 计算,其结果会如何?由数据表一计算得出数据表三。 计算,其结果会如何?由数据表一计算得出数据表三。
数据表三
g
|
第1次
|
第2次
|
第3次
|
第4次
|
第5次
|
第6次
|
平均值
|
漏了半径
|
9.61m/s2
|
9.59 m/s2
|
9.61 m/s2
|
9.67 m/s2
|
9.65 m/s2
|
9.70 m/s2
|
9.64 m/s2
|
加了半径
|
9.82 m/s2
|
9.75 m/s2
|
9.75 m/s2
|
9.80 m/s2
|
9.76 m/s2
|
9.80 m/s2
|
9.78 m/s2
|
加了直径
|
10.02 m/s2
|
9.92 m/s2
|
9.89 m/s2
|
9.93 m/s2
|
9.87 m/s2
|
9.90 m/s2
|
9.92 m/s2
|
漏了半径和多加了半径相对标准处理(即加半径)的绝对误差都为0.14 m/s2、相对误差也都是1.43%,误差不大,可毕竟还是存在的。因此,用单摆测重力加速度建议用T2-l图象处理。
【习题二】为估算某山顶高度,某同学爬到该座山顶,他用单摆测出其周期为T,然后他把此单摆拿到海平面处测得周期为T0,他查表得知地球的半径为R,由此他估算出山顶到海平面的高度。试分析他是如何估算的。
理论分析:这是一道经典的简谐振动与万有引力相结合的习题。设摆长为l,山顶重力加速度为g,则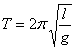 ;单摆移到海平面时重力加速度为g0,则 ;单摆移到海平面时重力加速度为g0,则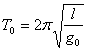 。设地球质量为M,摆球质量为m,山顶距离海平面高度为h,忽略地球自转影响,则有:在山顶上 。设地球质量为M,摆球质量为m,山顶距离海平面高度为h,忽略地球自转影响,则有:在山顶上  ;在海平面处 ;在海平面处 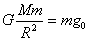 。由上述各式解得 。由上述各式解得  。这种方法能测出山顶的高度吗?笔者带领学生在我校六层楼高的科技楼进行了实测。 。这种方法能测出山顶的高度吗?笔者带领学生在我校六层楼高的科技楼进行了实测。
数据表四(摆线长60.62cm,摆球半径1.00cm)
|
第一层
|
第五层
|
全振动次数n
|
50
|
50
|
50
|
平均值
|
50
|
50
|
50
|
平均值
|
时间t/s
|
78.79
|
78.79
|
78.83
|
78.84
|
78.78
|
78.80
|
周期T/s
|
1.5758
|
1.5758
|
1.5766
|
1.5768
|
1.5756
|
1.5760
|
g/m·s-2
|
9.78676
|
9.78676
|
9.77683
|
9.78345
|
9.77435
|
9.78924
|
9.78427
|
9.78262
|
由上面的理论分析知: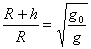 ,查得海平面处重力加速度标准参考值9.80665 m/s2,地球的半径平均值6370km,计算出第一层离海平面的高度h1=7.54828km,第五层离海平面的高度h2=7.81883km,高度差Δh=h2-h1=270.55m,与实际楼层高相差太大!通过找有关资料得知我县城的海拔高度约为300m,与计算得出的7km多米海拔高度也相差很大。原因有二:一是偶然误差造成的,主要是测定单摆的周期不够准确;二是系统误差造成的,单摆结合万有引力计算海拔高度的方法不完善,主要原因是没有考虑地球的自转。那种误差是主要因素?以世界最高峰──珠穆朗玛峰为例,海拔高度为8848m,通过计算得出其顶峰的重力加速度为9.77946m/s2,与海平面处重力加速度标准参考值相差不大,更何况在一般的山顶,因此主要误差来源应该是系统误差,用这种方法测山顶的海拔高度的可行性值得怀疑。 ,查得海平面处重力加速度标准参考值9.80665 m/s2,地球的半径平均值6370km,计算出第一层离海平面的高度h1=7.54828km,第五层离海平面的高度h2=7.81883km,高度差Δh=h2-h1=270.55m,与实际楼层高相差太大!通过找有关资料得知我县城的海拔高度约为300m,与计算得出的7km多米海拔高度也相差很大。原因有二:一是偶然误差造成的,主要是测定单摆的周期不够准确;二是系统误差造成的,单摆结合万有引力计算海拔高度的方法不完善,主要原因是没有考虑地球的自转。那种误差是主要因素?以世界最高峰──珠穆朗玛峰为例,海拔高度为8848m,通过计算得出其顶峰的重力加速度为9.77946m/s2,与海平面处重力加速度标准参考值相差不大,更何况在一般的山顶,因此主要误差来源应该是系统误差,用这种方法测山顶的海拔高度的可行性值得怀疑。
所以物理实验比物理习题具有更深远的物理意义。 (责任编辑:admin)
|



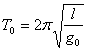 。设地球质量为M,摆球质量为m,山顶距离海平面高度为h,忽略地球自转影响,则有:在山顶上
。设地球质量为M,摆球质量为m,山顶距离海平面高度为h,忽略地球自转影响,则有:在山顶上