是巧合还是必然
湖北省监利县朱河中学 黄尚鹏
笔者在教学中发现这样一道题目:如图所示,长为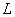 、电阻为 、电阻为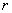 、质量为 、质量为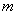 的金属棒 的金属棒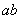 垂直跨搁在位于水平面上的两条平行的光滑金属导轨上,两导轨的间距也为 垂直跨搁在位于水平面上的两条平行的光滑金属导轨上,两导轨的间距也为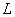 ,棒与导轨间接触良好,导轨电阻不计,导轨左端接有电阻 ,棒与导轨间接触良好,导轨电阻不计,导轨左端接有电阻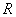 。整个装置处在垂直于导轨平面向里的磁感应强度为 。整个装置处在垂直于导轨平面向里的磁感应强度为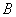 的匀强磁场中,现给金属棒一水平向右的初速度 的匀强磁场中,现给金属棒一水平向右的初速度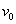 ,求金属棒能够运动的最大位移 ,求金属棒能够运动的最大位移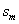 。 。
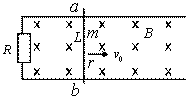
这道题常规的正确解法如下:
解1:金属棒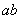 向右切割磁感线产生感应电流,感应电流 向右切割磁感线产生感应电流,感应电流
受到向左的安培力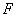 ,故 ,故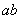 将做减速运动直到停止。 将做减速运动直到停止。
根据动量定理有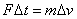 ,即 ,即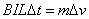 ,对该式两边求和 ,对该式两边求和
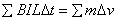 , ,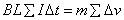 ,即 ,即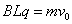
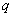 即为整个过程中通过电阻 即为整个过程中通过电阻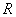 的电荷量,且 的电荷量,且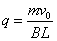 (1) (1)
另一方面,整个过程由法拉第电磁感应定律有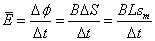
故整个过程中通过电阻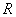 的电荷量 的电荷量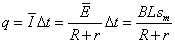 (2) (2)
联立(1)(2)解得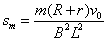
但笔者发现有部分学生用动能定理求解,过程如下:
解2:初始时刻金属棒受安培力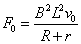 ,金属棒停止运动时受安培力 ,金属棒停止运动时受安培力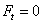
故整个过程安培力的平均值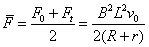 ,根据动能定理有 ,根据动能定理有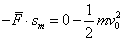
解得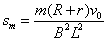 ,与解法1得出的答案完全相同。 ,与解法1得出的答案完全相同。
不难看出,解法1通过两种不同的途径计算整个过程中通过电阻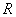 的电荷量,从而建立等式使问题圆满解决。解法2应用平均值巧妙地得出了答案,但解法2令人心存疑惑,即安培力的平均值 的电荷量,从而建立等式使问题圆满解决。解法2应用平均值巧妙地得出了答案,但解法2令人心存疑惑,即安培力的平均值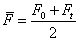 算法可靠吗?理论依据是什么?我们知道,在动能定理中, 算法可靠吗?理论依据是什么?我们知道,在动能定理中,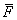 应该是力对位移的平均值,公式 应该是力对位移的平均值,公式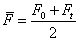 只适用于 只适用于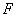 与 与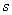 为线性关系这种情况,但这两者是否一定为线性关系,解法2能得出正确答案是一种巧合还是一种必然呢?下面笔者将证明 为线性关系这种情况,但这两者是否一定为线性关系,解法2能得出正确答案是一种巧合还是一种必然呢?下面笔者将证明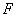 与 与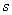 的确为线性关系。 的确为线性关系。
证明:安培力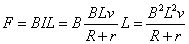 ,根据动量定理有 ,根据动量定理有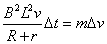 ,可得 ,可得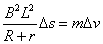 ,即 ,即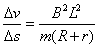 为常量,故速度 为常量,故速度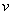 随位移 随位移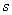 均匀变化, 均匀变化,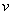 与 与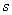 为线性关系,考虑到速度随位移逐渐减小且初始时刻位移为零速度为 为线性关系,考虑到速度随位移逐渐减小且初始时刻位移为零速度为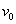 ,故速度 ,故速度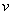 与位移 与位移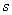 的关系可表示为 的关系可表示为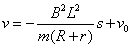 ,因此安培力 ,因此安培力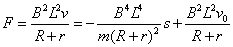 , ,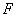 与 与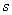 为线性关系,证毕。 (责任编辑:admin) 为线性关系,证毕。 (责任编辑:admin)
|
