天体运动中的几个“另类”问题
http://www.newdu.com 2025/05/24 04:05:26 人民教育出版社 佚名 参加讨论
天体运动中的几个“另类”问题 江苏省靖江市季市中学 范晓波 天体运动部分的绝大多数问题,解决的原理及方法比较单一,处理的基本思路是:将天体的运动近似看成匀速圆周运动,根据万有引力提供向心力列方程,向心加速度按涉及的运动学量选择相应的展开形式。 如有必要,可结合黄金代换式 一、变轨问题 例:某人造卫星因受高空稀薄空气的阻力作用,绕地球运转的轨道会慢慢改变。每次测量中卫星的运动可近似看作圆周运动,某次测量卫星的轨道半径为 A. B. C. D. 分析:空气阻力作用下,卫星的运行速度首先减小,速度减小后的卫星不能继续沿原轨道运动,由于 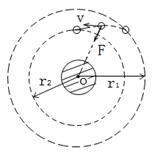 如图,近(向)心运动过程中万有引力方向与卫星运动方向不垂直,会让卫星加速,速度增大(从能量角度看,万有引力对卫星做正功,卫星动能增加,速度增大),且增加的数值超过原先减少的数值。所以 解:应选C选项。 说明:本题如果只注意到空气阻力使卫星速度减小的过程,很容易错选B选项,因此,分析问题一定要全面,切忌盲目下结论。 卫星从椭圆轨道变到圆轨道或从圆轨道变到椭圆轨道是卫星技术的一个重要方面,卫星定轨和返回都要用到这个技术。  以卫星从椭圆远点变到圆轨道为例加以分析:如图,在轨道远点,万有引力 二、双星问题 例:在天体运动中,将两颗彼此相距较近的行星称为双星。它们在相互的万有引力作用下间距保持不变,并沿半径不同的同心圆轨道做匀速圆周运动。如果双星间距为 分析:双星系统中,两颗星球绕同一点做匀速圆周运动,且两者始终与圆心共线,相同时间内转过相同的角度,即角速度相等,则周期也相等。但两者做匀速圆周运动的半径不相等。  解:设行星转动的角速度为 (1)如图,对星球 同理对星球 两式相除得: 又因为 所以 (2)因为 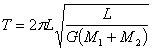 (3)因为 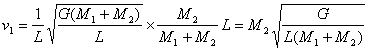  说明:处理双星问题必须注意两点(1)两颗星球运行的角速度、周期相等;(2)轨道半径不等于引力距离(这一点务必理解)。弄清每个表达式中各字母的含义,在示意图中相应位置标出相关量,可以最大限度减少错误。 三、追及问题 例:两颗卫星在同一轨道平面内绕地球做匀速圆周运动,地球半径为 分析:两卫星周期之比可按基本思路处理;要求  解:(1)对做匀速圆周运动的卫星使用向心力公式 可得: 所以 (2)由 设经过时间 其中 而 所以 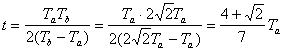 说明:圆周运动中的追及和相遇问题也应“利用(角)位移关系列方程”。当然,如果能直接将角位移关系转化成转动圈数关系,运算过程更简洁,但不如利用角位移关系容易理解,而且可以和直线运动中同类问题的解法统一起来,记忆比较方便。常见情况下的角位移关系如下,请自行结合运动过程示意图理解。设  四、超失重问题 例:某物体在地面上受到的重力为 分析:物体具有竖直向上的加速度,处于超重状态,物体对支持物的压力大于自身实际重力;而由于高空重力加速度小于地面重力加速度,同一物体在高空的实际重力又小于在地面的实际重力。  解:如图,设此时火箭离地球表面的高度为 根据超、失重观点有 可得  而由 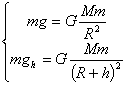 可知: 可知:所以  说明:航天器在发射过程中有一个向上加速运动阶段,在返回地球时有一个向下减速阶段,这两个过程中航天器及内部的物体都处于超重状态;航天器进入轨道作匀速圆周运动时,由于万有引力(重力)全部提供向心力,此时航天器及内部的所有物体都处于完全失重状态。 既掌握基本问题的处理方法,又熟悉“另类”问题的分析要点,这样在面对天体运动问题时才能应付自如。 五、变式练习 1.开普勒三定律也适用于神舟七号飞船的变轨运动。飞船与火箭分离后进入预定轨道,飞船在近地点(可认为近地面)开动发动机加速,之后,飞船速度增大并转移到与地球表面相切的椭圆轨道,飞船在远地点再次点火加速,飞船沿半径为  2.两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R,其运动周期为T,求两星的总质量。 3.如图所示,  4.北京时间9月27日17时,航天员翟志刚在完成一系列空间科学实验,并按预定方案进行太空行走后,安全返回神舟七号轨道舱,这标志着我国航天员首次空间出舱活动取得成功。若这时神舟七号在离地面高为 5.为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住长降机。放开绳,升降机能到达地球上;人坐在升降机里,在卫星上通过电动机把升降机拉到卫星上。已知地球表面的重力加速 (1)某人在地球表面用体重计称得重 (2)如果把绳的一端搁置在同步卫星上,地球自转的周期为 变式练习答案: 1. 2. 3.(1) 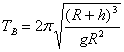 (2) (2)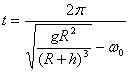 4.(1)航天员对神舟七号的压力为零。因为地球对航天员的万有引力恰好提供了航天员随飞船绕地球做匀速圆周运动所需的向心力,航天员处于完全失重状态;(2) 5.(1) |
- 上一篇:“平抛运动”专项训练
- 下一篇:天体运动中的追及相遇问题