平抛运动的三个推论及其应用
http://www.newdu.com 2025/05/25 06:05:41 人民教育出版社 佚名 参加讨论
平抛运动的三个推论及其应用 江西省临川二中 周 勇 平抛运动是一种匀变速曲线运动，根据其运动性质，轨迹、特点等，归纳出以下三个简捷实用的推论。 一、推论一：速度偏向角的函数值规律：平抛运动任意时刻的速度偏向角的三种函数值分别为，如图所示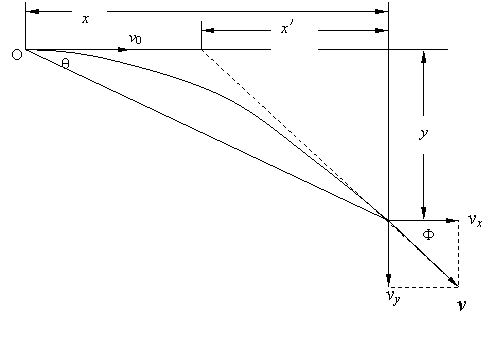：     式中  表示速度V的竖起分量， 、 表示速度V的水平分量，x、y分别表示水平和竖直位移。例1 在平面直角坐标系xOy中，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于Y轴射入电场，经x轴上的N点与x轴正方向成θ=60°角射入磁场，最后从y轴负半轴上的P点垂直于Y轴射出磁场，如图所示。不计粒子重力，求： （1）M、N两点间的电势差UMN； （2）粒子在磁场中运动的轨道半径r； （3）粒子从M点运动到P点的总时间t。 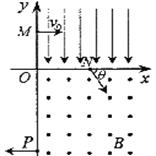 解析：粒子在第Ⅰ象限内，只在电场力的作用下做类平抛运动，设粒子过N点时的速度为v，则有推论一有  ①解得  ②粒子从M点运动到N点的过程中，有动能定理得  ③由（2）（3）两式得  ④（2）（3）两问的解答略，请读者分析。 例2 如图所示，在xOy平面的第一象限有一匀强电场，电场的方向平行于y轴向下；在x轴和第四象限的射线OC之间有一匀强磁场，磁感应强度的大小为B，方向垂直于纸面向外。有一质量为m，带有电荷量+q的质点由电场左侧平行于x轴射入电场。质点到达x轴上A点时，速度方向与x轴的夹角  ，A点与原点O的距离为d。接着，质点进入磁场，并垂直于OC飞离磁场。不计重力影响。若OC与x轴的夹角为，求（1）粒子在磁场中运动速度的大小： （2）匀强电场的场强大小。 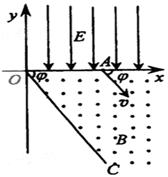 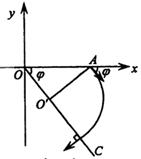 解析：（1）质点在磁场中的只要洛仑兹力作用下做匀速圆周运动，根据飞进和飞离磁场的方向，进而确定圆心，进而确定圆心O＇和半径R，如图所示则有 R=dsin ① 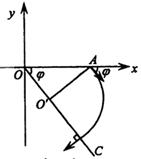 由洛化兹力公式和牛顿第二定律得  ②由①②式，得 ③（2）质点在电场中的运动为类平抛运动。由推论一有 x=v0t ④ v0＝vcos? ⑤ vsin?＝at ⑥ 式中v0表示射入电场的速度，a表示在电场中的加速度，t为电场中运动时间。设 电场强度为E，由牛顿第二定律得： qE＝ma ⑦ 由④⑤⑥⑦得  ⑧二、推论二：速度偏向角与位移偏向向角的关系：平抛运动的速度偏向角的正切函数  ，等于位移偏向角θ（合位移S与水平位移x的夹角）的正切函数值2倍，即 例3 如图所示，一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足（ ） A．tanφ=sinθ B．tanφ=cosθ C．tanφ=tanθ D．tanφ=2tanθ 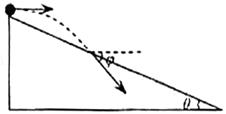 解析：题中φ的为速度偏向角，θ角与位移偏向角相等，由平抛运动推论二可得正确选项D，本题关键应记住推论，把斜面倾角转化为位移偏向角 利用该推论可迅速解决例2的第（2）问。设质点飞入电场时距O点距离为L，由几何关系和推论二有  （θ为位移偏向角） ① ②由动能定理得  ③由①②③式得  三、推论三：速度方向反向延长线规律：平抛运动任意时刻的瞬时速度方向的反向延长线，一定通过此时水平位移x的中点 即  。例4 如图所示，真空室中电极K发出的电子（初速不计）经过U0=1000V的加速电场后，由小孔S沿两水平金属板A、B间的中心线射入。A、B板长l=0．20m，相距d=0．020m，加在A、B两板间的电压u随时间t变化如图所示。设A、B间的电场可看作是均匀的，且两板外无电场。在每个电子通过电场区域的极短时间内，电场可视作恒定的。两板右侧放一记录圆筒，筒在左侧边缘与极板右端距离b=0．15m，筒绕其竖直轴匀速转动，周期T=0．20s，筒的周长s=0．20m，筒能接收到通过A、B板的全部电子。 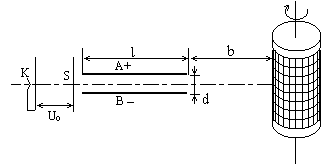 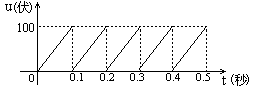 （1）以t=0时（见图，此时u=0）电子打到圆筒记录纸上的点作为x、y坐标系的原点，并取y轴竖直向上。试计算电子打到记录纸上的最高点的y坐标和x坐标。（不计重力作用） （2）略 解析：设电子打在记录纸上最高点的坐标为y，如图所示，由推论三和三角形相似可得 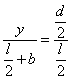 解得：  可见利用平抛（类平抛）运动的推论可迅速得到答案，关于坐标x的求解笔者在此不再赘述，敬请读者分析 总上所述，这几道题从不同层次、角度和侧面考查了平抛运动，考查了学生灵活运用学知识的能力。本文就平抛运动的研究提供给读者一个案例，抛砖引玉，希望能给读者研究其它知识点产生一点启发。 (责任编辑：admin) |
- 上一篇：一道运动学高考题的几种解法
- 下一篇：开普勒定律的推导及应用